Определитель матрицы.

Матрицы, основные понятия.

Матрицей размера m×n называется прямоугольная таблица чисел, содержащая m строк и n столбцов. Числа, составляющие матрицу, называются элементами матрицы.

Матрицы обозначаются прописными (заглавными) буквами латинского алфавита, например, A, B, C, …, а для обозначения элементов матрицы используются строчные буквы с двойной индексацией: a_ij, где i – номер строки, j – номер столбца.

Например, матрица

или, в сокращенной записи, A =(a_ij); i = 1, 2, …, m; j = 1, 2, …, n.

Алгебра матриц.

1. Умножение матрицы на число. Произведением матрицы A на число λ называется матрица B=λA, элементы которой b_ij=λa_ij для i = 1, 2, …, m; j = 1, 2, …, n.

Например, если , то .

Следствие. Общий множитель всех элементов матрицы можно выносить за знак матрицы.

Например, .

В частности, произведение матрицы A на число 0 есть нулевая матрица, т.е. 0• A =0.

2. Сложение матриц. Суммой двух матриц A и B одинакового размера m×n называется матрица C = A + B, элементы которой c_ij = a_ij + b_ij для i = 1, 2, …, m; j = 1, 2, …, n (т.е. матрицы складываются поэлементно).

Например, , , .

В частном случае A +0= A.

3. Вычитание матриц. Разность двух матриц одинакового размера определяется через предыдущие операции: A – B = A +(–1)• B.

4. Умножение матриц. Умножение матрицы A на матрицу B определено, когда число столбцов первой матрицы равно числу строк второй. Тогда произведением матриц A • B называется такая матрица C, каждый элемент которой c_ij равен сумме произведений элементов i -й строки матрицы A на соответствующие элементы j -го столбца матрицы B:

, i = 1, 2, …, m; j = 1, 2, …, n.

5. Возведение в степень. Целой положительной степенью A^m (m >1) квадратной матрицы A называется произведение m матриц, равных A, т.е.

.

Операция возведения в степень определяется только для квадратных матриц.

6. Транспонирование матрицы – переход от матрицы A к матрице A', в которой строки и столбцы поменялись местами с сохранением порядка. Матрица A' называется транспонированной относительно матрицы A:

, .

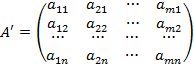Из определения следует, что если матрица A имеет размер m×n, то транспонированная матрица A' имеет размер n×m.

Например, ; .

Определитель матрицы.

Определителем квадратной матрицы n -го порядка, или определителем n -го порядка, называется число, равное алгебраической сумме n! членов, каждый из которых является произведением n элементов матрицы, взятых по одному из каждой строки и каждого столбца, причем знак каждого члена определяется как (–1) ^{r ( J )}, где r(J) – число инверсий в перестановке J из номеров столбцов элементов матрицы, если при этом номера строк записаны в порядке возрастания:

где сумма берется по всем перестановкам J.

Не нашли, что искали? Воспользуйтесь поиском: