Модуль вектора и его направляющие косинусы.

Множество векторов на прямой назовем одномерным векторным пространством R ¹, множество векторов на плоскости – двумерным векторным пространством R ², в пространстве – трехмерным векторным пространством R ³. Пространство Rⁿ является системой содержащей всю бесконечную совокупность -мерных векторов.

В пространстве R ³ обычно используют прямоугольную декартову систему координат Oxyz, где любая точка M пространства, имеющая координаты x (абсциссу), y (ординату) и z (аппликату), обозначается M (x, y, z).

Определение. Вектор , начало которого находится в начале координат, а конец в точке A (x ₁, y ₁, z ₁), называют радиус-вектором точки A и обозначают или просто . Так как его координаты совпадают с координатами точки A, то его разложение по ортам имеет вид .

Вектор , имеющий начало в (∙) A (x ₁, y ₁, z ₁), и конец в (∙) B (x ₂, y ₂, z ₂), может быть записан в виде , где – радиус-вектор точки B; – радиус-вектор точки A.

Поэтому разложение вектора по ортам имеет вид:

Его длина равна расстоянию между точками A и B:

Свободный вектор, например 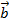, заданный в координатном пространстве Oxyz, может быть представлен в виде , где b_x, b_y, b_z – проекции вектора 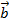на соответствующие оси координат (координаты вектора), а , , – орты этих осей. Пишут .

Длина вектора (модуль вектора) определяется по формуле:

Направление вектора определяется углами a, b, g, образованными им с осями координат Ox, Oy, Oz. Косинусы этих углов (направляющие косинусы вектора) вычисляются по формулам:

Тогда координаты вектора будут равны:

Подставив эти выражения в формулу вычисления длины вектора, установим, что направляющие косинусы вектора связаны соотношением:

Замечание. Координатами единичного вектора являются числа cosa, cosb, cosg, то есть .

Не нашли, что искали? Воспользуйтесь поиском: