
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Признак параллельности прямой и плоскости
Теорема
Если прямая, не принадлежащая плоскости, параллельна какой-нибудь прямой в этой плоскости, то она параллельна и самой плоскости.

Доказательство
Пусть α - плоскость, a – не лежащая в ней прямая и a1 – прямая в плоскости α, параллельная прямой a. Проведем плоскость α1 через прямые a и a1. Плоскости α и α1 пересекаются по прямой a1. Если бы прямая a пересекала плоскость α, то точка пересечения принадлежала бы прямой a1. Но это невозможно, так как прямые a и a1 параллельны. Следовательно, прямая a не пересекает плоскостью α, а значит, параллельна плоскости α. Теорема доказана.
| Признак параллельности прямой и плоскости Теорема. Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна данной плоскости. |

|
| Теорема. Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой. Теорема.Если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая либо также параллельна данной плоскости, либо лежит в этой плоскости. |

|
18. ПЛОСКОСТЕЙ
Если две параллельные плоскости пересекаются третьей, то прямые пересечения параллельны (рис. 333).
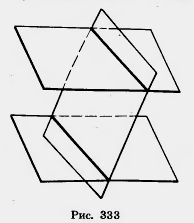
Действительно, согласно определению параллельные прямые — это прямые, которые лежат в одной плоскости и не пересекаются. Наши прямые лежат в одной плоскости — секущей плоскости. Они не пересекаются, так как не пересекаются содержащие их параллельные плоскости.
Значит, прямые параллельны, что и требовалось доказать
Свойства
§ Если плоскость α параллельна каждой из двух пересекающихся прямых, лежащих в другой плоскости β, то эти плоскости параллельны
§ Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны
§ Через точку вне данной плоскости можно провести плоскость, параллельную данной, и притом только одну
§ Отрезки параллельных прямых, ограниченные двумя параллельными плоскостями, равны
§ Два угла с соответственно параллельными и одинаково направленными сторонами равны и лежат в параллельных плоскостях
19. 
20.

Если две прямые лежат в одной плоскости, угол между ними легко измерить — например, с помощью транспортира. А как измерить угол между прямой и плоскостью?
Пусть прямая пересекает плоскость, причем не под прямым, а под каким-то другим углом. Такая прямая называется наклонной.
Опустим перпендикуляр из какой-либо точки наклонной на нашу плоскость. Соединим основание перпендикуляра с точкой пересечения наклонной и плоскости. Мы получили проекцию наклонной на плоскость.

Угол между прямой и плоскостью — это угол между прямой и ее проекцией на данную плоскость.
Обратите внимание — в качестве угла между прямой и плоскостью мы выбираем острый угол.
Если прямая параллельна плоскости, значит, угол между прямой и плоскостью равен нулю.
Если прямая перпендикулярна плоскости, ее проекцией на плоскость окажется точка. Очевидно, в этом случае угол между прямой и плоскостью равен 90°.
Прямая перпендикулярна плоскости, если она перпендикулярна любой прямой, лежащей в этой плоскости.
Это определение. Но как же с ним работать? Как проверить, что данная прямая перпендикулярна всем прямым, лежащим в плоскости? Ведь их там бесконечно много.
На практике применяется признак перпендикулярности прямой и плоскости:
Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в этой плоскости.

21.Двугранный угол — пространственная геометрическая фигура, образованная двумя полуплоскостями, исходящими из одной прямой, а также часть пространства, ограниченная этими полуплоскостями.[1]
Две плоскости называются перпендикулярными, если двугранный угол между ними равен 90 градусам.
§ Если плоскость проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.
§ Если из точки, принадлежащей одной из двух перпендикулярных плоскостей, провести перпендикуляр к другой плоскости, то этот перпендикуляр полностью лежит в первой плоскости.
§ Если в одной из двух перпендикулярных плоскостей провести перпендикуляр к их линии пересечения, то этот перпендикуляр будет перпендикулярен второй плоскости.
Две пересекающиеся плоскости образуют четыре двугранных угла с общим ребром: пары вертикальных углов равны, а сумма двух смежных углов равна 180°. Если один из четырех углов прямой, то три остальных также равны и прямые. Две плоскости называются перпендикулярными, если угол между ними прямой.
Теорема. Если плоскость проходит через прямую, перпендикулярную к другой плоскости, то эти плоскости перпендикулярны.
Пусть  и
и  - две плоскости такие, что
- две плоскости такие, что  проходит через прямую АВ, перпендикулярную к
проходит через прямую АВ, перпендикулярную к  и пересекающуюся с ней в точке А (рис. 49). Докажем, что
и пересекающуюся с ней в точке А (рис. 49). Докажем, что  _|_
_|_  . Плоскости
. Плоскости  и
и  пересекаются по некоторой прямой AC, причем AВ _|_ AC, т.к. AB _|_
пересекаются по некоторой прямой AC, причем AВ _|_ AC, т.к. AB _|_  . Проведем в плоскости
. Проведем в плоскости  прямую AD, перпендикулярную прямой АС.
прямую AD, перпендикулярную прямой АС.

Тогда угол BAD — линейный угол двугранного угла, образованного  и
и  . Но < ВАD - 90° (ибо AB _|_
. Но < ВАD - 90° (ибо AB _|_  ), а тогда, по определению,
), а тогда, по определению,  _|_
_|_  . Теорема доказана.
. Теорема доказана.
22. Многогранником называется такое тело, поверхность которого состоит из конечного числа плоских многоугольников.
.
1. любого из многоугольников, составляющих многогранник, можно дойти до любого из них, переходя к смежному с ним, а от этого, в свою очередь, к смежному с ним, и т. д.
Эти многоугольники называются гранями, их стороны — рёбрами, а их вершины — вершинами многогранника. Простейшими примерами многогранников являются выпуклые многогранники, то есть граница ограниченного подмножества евклидова пространства являющееся пересечением конечного числа полупространств.
Приведенное определение многогранника получает различный смысл в зависимости от того, как определить многоугольник, для которого возможны следующие два варианта:
§ Плоские замкнутые ломаные (хотя бы и самопересекающиеся);
§ Части плоскости, ограниченные ломаными.
В первом случае мы получаем понятие звёздчатый многогранник. Во втором — многогранник есть поверхность, составленная из многоугольных кусков. Если эта поверхность сама себя не пересекает, то она есть полная поверхность некоторого геометрического тела, которое также называется многогранником. Отсюда возникает третье определение многогранника, как самого геометрического тела
23.
Прямая призма

Призма называется прямой, если ее боковые ребра перпендикулярны основаниям.
Призма называется наклонной, если ее боковые ребра не перпендикулярны основаниям.
У прямой призмы грани – прямоугольники.

Призма называется правильной, если ее основания являются правильными многоугольниками.
Площадью боковой поверхности призмы называется сумма площадей боковых граней.
Полная поверхность призмы равна сумме боковой поверхности и площадей оснований
Элементы призмы:
Точки  — называются вершинами
— называются вершинами
Отрезки  называются боковыми ребрами
называются боковыми ребрами
Многоугольники 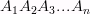 и
и 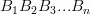 — называютсяоснованиями. Также основаниями называют сами плоскости
— называютсяоснованиями. Также основаниями называют сами плоскости  и
и 

24. Параллелепи́пед (от греч. παράλλος — параллельный и греч. επιπεδον — плоскость) — призма, основанием которой служитпараллелограмм, или (равносильно) многогранник, у которого шесть граней и каждая из них параллелограмм.
§ Параллелепипед симметричен относительно середины его диагонали.
§ Любой отрезок с концами, принадлежащими поверхности параллелепипеда и проходящий через середину его диагонали, делится ею пополам; в частности, все диагонали параллелепипеда пересекаются в одной точке и делятся ею пополам.
§ Противолежащие грани параллелепипеда параллельны и равны.
§ Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений.
Площадь поверхности прямоугольного параллелепипеда равна удвоенной сумме площадей трех граней этого параллелепипеда:
| 1. | S = 2(Sa + Sb + Sc)= 2(ab + bc + ac) |
25. Пирамида и ее элементы
.
Рассмотрим плоскость  , многоугольник
, многоугольник 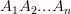 , лежащий в ней и точку S, не лежащую в ней. Соединим S со всеми вершинами многоугольника. Полученный при этом многогранник называется пирамидой. Отрезки
, лежащий в ней и точку S, не лежащую в ней. Соединим S со всеми вершинами многоугольника. Полученный при этом многогранник называется пирамидой. Отрезки  называются боковыми ребрами.
называются боковыми ребрами.  Многоугольник называется основанием, а точка S — вершиной пирамиды. В зависимости от числа n пирамида называется треугольной (n=3), четырехугольной (n=4), птяиугольной (n=5) и так далее. Альтернативное название треугольной пирамиды – тетраэдр. Высотой пирамиды называется перпендикуляр, опущенный из ее вершины к плоскости основания.
Многоугольник называется основанием, а точка S — вершиной пирамиды. В зависимости от числа n пирамида называется треугольной (n=3), четырехугольной (n=4), птяиугольной (n=5) и так далее. Альтернативное название треугольной пирамиды – тетраэдр. Высотой пирамиды называется перпендикуляр, опущенный из ее вершины к плоскости основания.
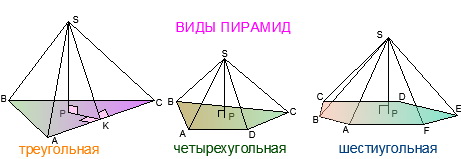
Пирамида называется правильной, если 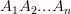 правильный многоугольник, а основание высоты пирамиды (основание перпендикуляра) является его центром.
правильный многоугольник, а основание высоты пирамиды (основание перпендикуляра) является его центром.
Программа предназначена для расчета площади боковой поверхности правильной пирамиды.
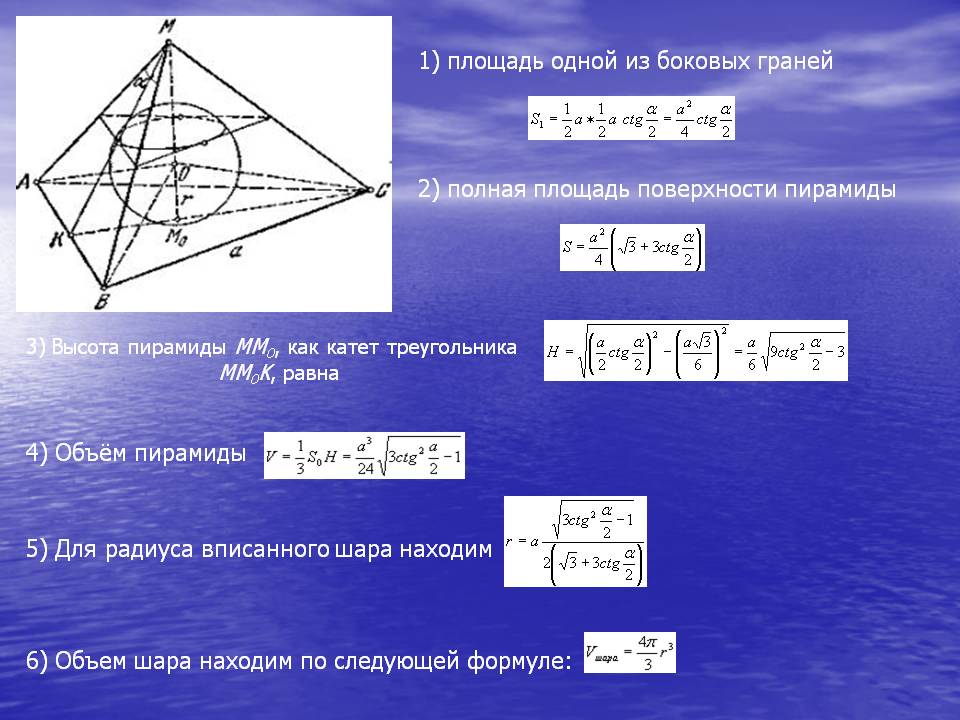
Пирамида является многогранником, имеющим основание в виде многоугольника, а остальные грани являются треугольниками с общей вершиной.

Формула для вычисления площади боковой поверхности правильной пирамиды:

где p - периметр основания (многоугольника ABCDE),
а - апофема (OS);
Апофемой называется высота боковой грани правильной пирамиды, которая проведена из её вершины.
Чтобы найти площадь боковой поверхности правильной пирамиды, введите значения периметра пирамиды и апофемы, затем нажмите кнопку "ВЫЧИСЛИТЬ".Программа определит площадь боковой поверхности правильной пирамиды, значение которой может быть помещено в буфер обмена.
Усеченная пирамида
| Усеченной пирамидой называется часть полной пирамиды, заключенная между основанием и параллельным ему сечением. | |
| Сечение называют верхним основанием усеченной пирамиды, а основание полной пирамиды — нижним основанием усеченной пирамиды. (Основания подобны.) Боковые грани усеченной пирамиды — трапеции. В усеченной пирамиде 3 n ребер, 2 n вершин, n + 2 грани, n (n - 3) диагонали. Расстояние между верхним и нижним основаниями — высота усеченной пирамиды (отрезок, отсеченный от высоты полной пирамиды). | 
|
| Площадь полной поверхности усеченной пирамиды равна сумме площадей ее граней. | |
| Объем усеченной пирамиды (S и s - площади оснований, Н — высота) | 
|
26.
Телом вращения называется тело, образованное в результате вращения какой - либо линии вокруг прямой.
Прямой круговой цилиндр вписан в шар, если окружности его оснований лежат на сфере. Основания цилиндра являются малыми кругами шара, центр шара совпадает с серединой оси цилиндра. [ 2 ]
Прямой круговой цилиндр вписан в шар, если окружности его оснований лежат на сфере. Очевидно, центр шара лежит ни середине оси цилиндра. [ 3 ]
Объем всякого цилиндра равен произведению площади основания на высоту:
| 1. | V =π r 2 h |
Полная площадь поверхности цилиндра равна сумме боковой поверхности цилиндра и двойной площади основания цилиндра.
Формула для вычисления полной площади поверхности цилиндра:

27. Круглый конус может быть получен вращениемпрямоугольного треугольника вокруг одного из его катетов, поэтому круглый конус называют также конусом вращения. См. также Объем круглого конуса
Полная площадь поверхности круглого конуса равна сумме площадей боковой поверхности конуса и его основания. Основание конуса есть круг и его площадь вычисляется по формуле площади круга:
| 2. | S =π r l +π r 2=π r (r + l) |
28. Усеченный конус получится, если в конусе провести сечение, параллельное основанию. Тело ограниченное этим сечением, основанием и боковой поверхностью конуса называется усеченным конусом. См. также Объем усеченного конуса
Полная площадь поверхности усеченного конуса равна сумме площадей боковой поверхности усеченного конуса и его оснований. Основания усеченного конуса есть круги и их площадь вычисляется поформуле площади круга: S = π (r 12 + (r 1 + r 2) l + r 22)
29. Шар – геометрическое тело, ограниченное поверхностью, все точки которой находятся на равном расстоянии от центра. Это расстояние называется радиусом шара.
Сфе́ра (греч. σφαῖρα — мяч) — замкнутая поверхность, геометрическое место точек в пространстве, равноудалённых от данной точки, называемой центром сферы. Сфера является частным случаем эллипсоида, у которого все три оси (полуоси, радиусы) равны. Сфера является поверхностью шара.
Площадь сферической поверхности шарового сегмента (шарового сектора) и шарового слоя зависит только от их высоты и радиуса шара и равна длине окружности большого круга шара, умноженной на высоту
Объем шара равен объему пирамиды, основание которой имеет ту же площадь, что и поверхность шара, а высота есть радиус шара
Объем шара в полтора раза меньше, чем объем описанного вокруг него цилиндра.
Элементы шара
Шаровой сегмент
Секущая плоскость разбивает шар на два шаровых сегмента.
Н — высота сегмента, 0 < Н < 2 R,
r — радиус основания сегмента,
 Объем шарового сегмента
Объем шарового сегмента
 Площадь сферической поверхности шарового сегмента
Площадь сферической поверхности шарового сегмента

| 
|
| Шаровой слой Шаровым слоем называется часть шара, заключенная между двумя параллельными сечениями. Расстояние (Н) между сечениями называется высотой слоя, а сами сечения — основаниями слоя. Площадь сферической поверхности (объем) шарового слоя может быть найдена как разность площадей сферических поверхностей (объемов)шаровых сегментов. | 
|
30. Понятие вектора
Отрезок, для которого указано, какой из его концов считается началом, а какой — концом, называется вектором. Направление вектора (от начала к концу) на рисунках отмечается стрелкой. Любая точка пространства также может рассматриваться как вектор. Такой вектор называется нулевым. Начало и конец нулевого вектора совпадают, и он не имеет какого-либо определенного направления. Нулевой вектор обозначается символом 
|
10.1
1. Умножение вектора на число (рис. 56).
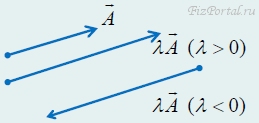
рис. 56
Произведением вектора А на число λ называется вектор В, модуль которого равен произведению модуля вектора А на модуль числа λ:

направление не изменяется, если λ > 0; изменяется на противоположное, если λ < 0. Если λ = −1, то вектор
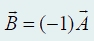
называется вектором, противоположным вектору А, и обозначается

2. Сложение векторов. Для того чтобы найти сумму двух векторов А и В вектор
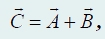
Тогда суммой будет вектор, начало которого совпадает с началом первого, а конец − с концом второго. Это правило сложения векторов называется «правилом треугольника» (рис. 57). необходимо изобразить векторы-слагаемые так, чтобы начало второго вектора совпадало с концом первого.
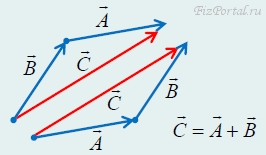
рис. 57
Легко доказать, что для векторов «от перемены мест слагаемых сумма не изменяется».
Укажем еще одно правило сложения векторов − «правило параллелограмма». Если совместить начала векторов-слагаемых и построить на них параллелограмм, то суммой будет вектор, совпадающий с диагональю этого параллелограмма (рис. 58).

рис. 58
Понятно, что сложение по «правилу параллелограмма» приводит к тому же результату, что и по «правилу треугольника».
«Правило треугольника» легко обобщить (на случай нескольких слагаемых). Для того чтобы найти сумму векторов

необходимо начало второго вектора совместить с концом первого, начало третьего − с концом второго и т. д. Тогда начало вектора С совпадет с началом первого, а конец С − с концом последнего (рис. 59).

рис. 59
3. Вычитание векторов. Операция вычитания сводится к двум предыдущим операциям: разностью двух векторов является сумма первого с вектором, противоположным второму:
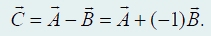
Можно также сформулировать «правило треугольника» для вычитания векторов: необходимо совместить начала векторов А и В, тогда их разностью будет вектор

проведенный от конца вектора В к концу вектора А (рис. 60).

рис. 60
В дальнейшем мы будем говорить о векторе перемещения материальной точки, то есть векторе, соединяющем начальное и конечное положения точки. Согласитесь, что введенные правила действия над векторами вполне очевидны для векторов перемещения.
4. Скалярное произведение векторов. Результатом скалярного произведения двух векторов А и В является число с, равное произведению модулей векторов на косинус угла α между
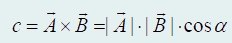

рис. 61
Операция скалярного произведения векторов очень широко используется в физике. В дальнейшем нам достаточно часто придется сталкиваться с такой операцией.
Не нашли, что искали? Воспользуйтесь поиском: