
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Предел функции в точке. Пусть функция f(x) определена в некоторой проколотой окрестности точки x0 .
Пусть функция f (x) определена в некоторой проколотой окрестности точки x 0.
Число A называется пределом функции f (x) при x → x 0 (или в точке x 0), если для любого ε > 0 найдется δ > 0 такое, что для всех x, для которых 0 < | x − x 0| < δ, справедливо неравенство
| f (x) − A | < ε, т.е.
| lim |
| x → x 0 |
f(x) = A ÜÞ " ε > 0 $ δ > 0: 0 < | x − x 0| < δ Þ | f (x) − A | < ε.
Используем понятие окрестности и учтем, что
0 < | x − x 0| < δ ÜÞ x Î
| · |
| O |
δ (x 0) и | f (x) − A | < ε ÜÞ f (x) Î Oε (A).
(Точка над символом окрестности указывает, что это проколотая окрестность.)
Теперь определение предела функции в точке можно представить в виде
f(x) = A ÜÞ " ε > 0 $ δ > 0: x Î
δ (x 0) Þ f (x) Î Oε (A). |
1. Арифметические свойства предела функции.
Пусть функции f и g определены на интервале (a, b), кроме быть может точки x 0. Если существует пределы
 и
и  ,
,
то существуют пределы в левых частях равенств и имеют место эти равенства:
a. 
б. 
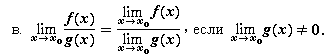
Эти свойства вытекают из определения Гейне предела функции и соответствующих свойств сходящихся последовательностей.
9. Непрерывная функция — функция без «скачков», то есть такая, у которой сколь угодно малые изменения аргумента приводят к сколь угодно малым изменениям значения функции.
Функцию y = f(x) называют непрерывной на отрезке [ a, b ], если она непрерывна во всех внутренних точках этого отрезка, а на его концах, т.е. в точках a и b, непрерывна соответственно справа и слева.
Функция f(x) непрерывна в точке  , принадлежащей области определения функции, если для любой последовательности значений аргумента, принадлежащей области определения и сходящейся к точке
, принадлежащей области определения функции, если для любой последовательности значений аргумента, принадлежащей области определения и сходящейся к точке  , последовательность соответствующих значений функции сходится к f(
, последовательность соответствующих значений функции сходится к f(  ).
).
Если функция f (x) не является непрерывной в точке x = a, то говорят, что f (x) имеет разрыв в этой точке. На рисунке 1 схематически изображены графики четырех функций, две из которых непрерывны при x = a, а две имеют разрыв.
10.Произво́дная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если такой предел существует. Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке). Процесс вычисления производной называется дифференци́рованием. Обратный процесс — интегрирование.
Не нашли, что искали? Воспользуйтесь поиском: