
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Системы линейных уравнений и неравенств с двумя переменными
Рассмотрим систему неравенств
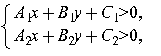
предполагая, что 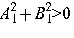 ,
, 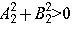 . Тогда неравенству
. Тогда неравенству 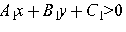 удовлетворяют точки множества
удовлетворяют точки множества 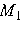 , лежащие по одну сторону от прямой
, лежащие по одну сторону от прямой 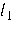 , заданной уравнением
, заданной уравнением  .
.
Аналогично множество 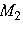 - одна из полуплоскостей, на которые разбивается координатная плоскость прямой
- одна из полуплоскостей, на которые разбивается координатная плоскость прямой 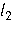 , заданной уравнением
, заданной уравнением  .
.
Множество решений системы 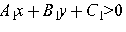 ,
,  представляет собой пересечение множеств
представляет собой пересечение множеств 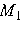 и
и 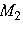 .
.
Аналогично решаются системы неравенств, получаемых из системы 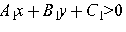 ,
,  заменой одного или двух знаков неравенств на противоположные.
заменой одного или двух знаков неравенств на противоположные.
Если пересекающиеся в точке 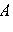 прямые
прямые 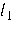 и
и 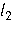 (рис. 1) задаются соответственно уравнениями
(рис. 1) задаются соответственно уравнениями
 и
и  , то неравенство
, то неравенство  определяет либо объединение одной пары
определяет либо объединение одной пары 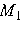 и
и 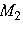 вертикальных углов с вершиной
вертикальных углов с вершиной 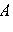 (рис. 1), либо объединение другой пары
(рис. 1), либо объединение другой пары 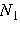 и
и 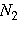 вертикальных углов с той же вершиной.
вертикальных углов с той же вершиной.
В самом деле, во всех точках каждого из множеств 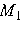 ,
, 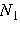 ,
, 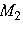 ,
, 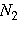 левая часть неравенства
левая часть неравенства  принимает либо положительные, либо отрицательные значения, а при переходе от одного из этих множеств к соседним (через одну из прямых
принимает либо положительные, либо отрицательные значения, а при переходе от одного из этих множеств к соседним (через одну из прямых 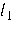 ,
, 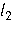 ) знак левой части этого неравенства меняется на противоположный.
) знак левой части этого неравенства меняется на противоположный.
Если, например, на множестве 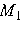 левая часть неравенства
левая часть неравенства  положительна, то на множествах
положительна, то на множествах 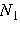 и
и 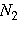 она будет отрицательной, а на
она будет отрицательной, а на 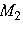 - положительной.
- положительной.
Чтобы определить, на каком из двух множеств  или
или 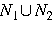 справедливо неравенство
справедливо неравенство  , достаточно определить знак левой части этого неравенства в какой-либо точке одного из множеств
, достаточно определить знак левой части этого неравенства в какой-либо точке одного из множеств 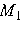 ,
, 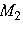 ,
, 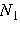 ,
, 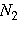 .
.
| 7.Бесконечные последовательности |
Функция f (n), определенная на множестве натуральных чисел, образует последовательность действительных чисел. Значения an = f (n), которые принимает эта функция, называются членами последовательности. Множество значений an = f (n) обозначается как { an }. Числовая последовательность { an } имеет предел L, если для каждого ε > 0 существует натуральное число N > 0, такое, что при всех n ≥ N выполняется неравенство 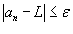 . В этом случае мы записываем . В этом случае мы записываем
 Числовая последовательность { an } имеет предел ∞, если для любого положительного числа M существует натуральное число N > 0, такое, что для всех n ≥ N справедливо неравенство an > M. В этом случае используется обозначение
Числовая последовательность { an } имеет предел ∞, если для любого положительного числа M существует натуральное число N > 0, такое, что для всех n ≥ N справедливо неравенство an > M. В этом случае используется обозначение
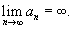 Если предел
Если предел 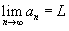 существует и L конечно, то говорят, что числовая последовательность сходится. В противном случае последовательность расходится. Теорема "о двух милиционерах": Предположим, что существует и L конечно, то говорят, что числовая последовательность сходится. В противном случае последовательность расходится. Теорема "о двух милиционерах": Предположим, что 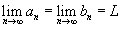 и { cn } является последовательностью, такой что и { cn } является последовательностью, такой что 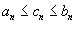 для всех n > N, где N − натуральное число. Тогда для всех n > N, где N − натуральное число. Тогда
 Последовательность { an } является ограниченной, если существует такое число M > 0, что | an | ≤ M для любого значения n. Если числовая последовательность сходится, то она ограничена. Любая неограниченная последовательность расходится. Последовательность { an } называется монотонно возрастающей, если an ≤ an+ 1 для всех n ≥ 1. Аналогично, последовательность { an } называется монотонно убывающей, если an ≥ an+ 1 для всех n ≥ 1. Последовательность { an } называется монотонной, если она монотонно возрастает или монотонно убывает.
Последовательность { an } является ограниченной, если существует такое число M > 0, что | an | ≤ M для любого значения n. Если числовая последовательность сходится, то она ограничена. Любая неограниченная последовательность расходится. Последовательность { an } называется монотонно возрастающей, если an ≤ an+ 1 для всех n ≥ 1. Аналогично, последовательность { an } называется монотонно убывающей, если an ≥ an+ 1 для всех n ≥ 1. Последовательность { an } называется монотонной, если она монотонно возрастает или монотонно убывает.
|
8.Числовая последовательность — это последовательность элементов числового пространства.
Числовые последовательности являются одним из основных объектов рассмотрения в математическом анализе.
Предел числовой последовательности — предел последовательности элементов числового пространства. Числовое пространство — это метрическое пространство, расстояние в котором определяется как модуль разности между элементами. Поэтому,
предел числовой последовательности — это такое число, что для всякой сколь угодно малой величины существует номер, начиная с которого уклонение членов последовательности от данной точки становится меньше заранее заданной величины.
Понятие предела последовательности вещественных чисел формулируется совсем просто, а в случае комплексных чисел существование предела последовательности равносильно существованию пределов соответствующих последовательностей вещественных и мнимых частей комплексных чисел.
Не нашли, что искали? Воспользуйтесь поиском: