Решение рациональных неравенств методом интервалов

Пример 1. Решить неравенство

В ответ запишите наибольшее целое решение неравенства.

Решение. Перенесем дробь из правой части в левую

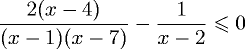
Приводим к общему знаменателю дроби в левой части неравенства.
Общим знаменателем будет произведение знаменателей дробей:
(x - 1)(x - 7)(x - 2). Для приведения к общему знаменателю умножим числетель и знаменатель первой дроби на (х - 2), а числитель и знаменатель второй дроби умножим на (х - 1)(х - 7).

Выполним действия (раскроем скобки) в числителе левой части:

2(x - 4)(x - 2) - (x - 1)(x - 7) = 2(x² - 6x + 8) - (x² - 8x + 7) = 2x² - 12x + 16 - x² + 8x - 7 = x² - 4x + 9.

Дискриминант многочлена x² - 4x + 9 равен 4² - 4·9 = 16 - 36 = -20 < 0. Поэтому разложить на множители числитель дроби нельзя.

Найдем нули числителя и знаменателя. Для этого решим уравнения для каждого множителя в числителе и знаменателе левой части:

x² - 4x + 9 = 0, решений нет,

х - 1 = 0, х = 1,

x - 7 = 0, x = 7,

x - 2 = 0, x = 2.

Наносим нули на числовую ось в порядке возрастания. Они разбивают ось на четыре интервала. Для каждого интервала определим знак левой части.

Для определения знака достаточно выбрать любое число из интервала и подставить в левую часть неравенства. Например, из интервала (2;7) выбираем число 3 и подставляем влеву часть неравенства в каждую из скобок:

x² - 4x + 9 > 0 (для всех значений х, так как дискримининтотрицателен);

x - 1 > 0 для х = 3,

х - 7 < 0 для х = 3,

х - 2 > 0 для х = 3.

Если число "минусов" (то есть отрицательных скобок) нечетно, то в итоге на интервале ставим "минус", если число "минусов" четно или они отсутствуют, то на интервале ставим знак "плюс". В нашем случае на интервале (2;7) ставим "минус".

Обратите внимание, что точки на кривой являются "выколотыми" (пустые кружочки). Так отмечаются на оси нули знаменателя левой части.

Теперь проведем через указанные точки кривую знаков (делать это необязательно):

Выбираем те интервалы, где кривая знаков проходит под числовой осью (там где стоят "минусы"): . Это и есть решение нашего неравенства.

Если бы знак неравенства будет другим (), то нужно выбирать интервалы, помеченные знаком "плюс".

Заметим, что число 7 не входит в решения системы (выколотая точка), поэтому самым большим целым числом входящим в множество решений будет число 6. Его и запишем в ответ задачи.

Ответ: 6.

Пример 2. Решить неравенство

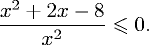
В ответ запишите сумму всех целых решений неравенства.

Решение. Разложим числитель левой части неравенства на скобки.
Для этого найдем решения уравнения.

x² + 2x - 8 = 0,

x₁ = -4, x₂ = 2.

Мы получим разложение на множители

x² + 2x - 8 = (x - x₁)(x - x₂) = (x + 4)(x - 2).

Найдем нули числителя и знаменателя: x₁ = -4, x₂ = 2, x₃ = 0.

Нанесем эти числа на ось, при этом нули знаменателя будут выколотыми точками, а нули числителя нет.

Расставим знаки на каждом интервале, с учетом того, что x² всегда больше или равен нуля. В результате должно получиться то, что изображено на рисунке выше.

Поскольку знак неравенства , то мы выбираем те интервалы, над которыми стоит знак "-".

Записываем решение неравенства, при этом выколотые точки соответсвуют круглым скобкам, а закрашенные точки соответсвуют квадратным скобкам.

.

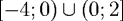Целые решения неравенства: -4, -3, -2, -1, 1, 2.

Их сумма равна -7.

Ответ: -7.

Не нашли, что искали? Воспользуйтесь поиском: