ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Определители третьего порядка
Метод подстановки.
1) Из одного уравнения выражаем одно из неизвестных, например x, через коэффициенты и другое неизвестное y:
x = (c – by) / a. (2)
2) Подставляем во второе уравнение вместо x:
d (c – by) / a + ey = f.
3) Решая последнее уравнение, находим y:
y = (af – cd) / (ae – bd).
4) Подставляем это значение вместо y в выражение (2):
x = (ce – bf) / (ae – bd).
Сложение или вычитание. Этот метод состоит в следующем.
1) Умножаем обе части 1-го уравнения системы (1) на (– d), а обе части 2-го уравнения на а и складываем их:
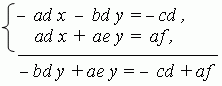
Отсюда получаем: y = (af – cd) / (ae – bd).
2) Подставляем найденное для y значение в любое уравнение системы (1):
ax + b(af – cd) / (ae – bd) = c.
3) Находим другое неизвестное: x = (ce – bf) / (ae – bd).
Определители третьего порядка
Пусть дана квадратная таблица из девяти чисел 
, 
, 
, 
, 
, 
, 
, 
, 
:
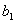. (1)
Определителем третьего порядка, соответствующим таблице (1), называется число, обозначаемое символом
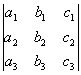
и определяемое равенством
. (2)
Числа , , , , , , 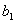, , называются элементами определителя. Элементы , , расположены на диагонали определителя, называемой главной; элементы , , составляют его побочную диагональ.
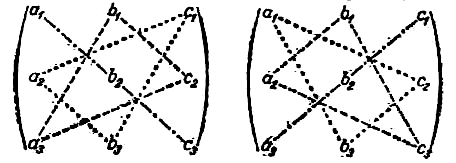
Чтобы получить следующие три члена правой части равенства (2), нужно перемножить элементы определителя по три так, как показано различными пунктирми на той же схеме справа, после чего у каждого из найденных произведений изменить знак.
3. Системы трёх линейных уравнений с тремя неизвестными имеют вид:
Решение этой системы может быть найдено теми же двумя основными методами, рассмотренными выше: подстановки и сложения или вычитания. Мы же рассмотрим здесь подробно только метод Крамера.
Во-первых, введём понятие определителя третьего порядка. Выражение
называется определителем третьего порядка.
Запоминать это выражение не нужно, так как его легко получить, если переписать таблицу (2), добавив справа первые два столбца. Тогда оно вычисляется путём перемножения чисел, расположенных на диагоналях, идущих от a, b, c – направо (со знаком «+») и от c, a, b – налево (со знаком «–»), и затем суммированием этих произведений:
Используя определитель третьего порядка (2), можно получить решение системы уравнений (1) в виде:
Эти формулы и есть правило Крамера для решения системы трёх линейных уравнений с тремя неизвестными.
П р и м е р. Решить методом Крамера систему трёх линейных уравнений с тремя неизвестными:
Р е ш е н и е. Введём следующие обозначения: D - знаменатель в формулах (4),
Dx, Dy, Dz – числители в выражениях для x, y, z – соответственно.
Тогда используя схему (3), получим:
отсюда по формулам Крамера (4): x = Dx / D = 0 / 32 = 0;
y = Dy / D = 32 / 32 = 1; z = Dz / D = 64 / 32 = 2.
4. Существуют различные приёмы решения систем уравнений.
Метод подстановки заключается в следующем:
- Одно из уравнений системы преобразуют к виду, в котором y выражено через х (или х через y);
- Полученное выражение подставляют вместо y (или вместо х) во второе уравнение. В результате получается уравнение с одной переменной;
- Находят корни этого уравнения;
- Воспользовавшись выражением y через х (или х через y), находят соответствующие значения х (или y).
Метод сложения основан на следующих теоремах:
- Пусть дана система двух уравнений с двумя переменными. Если одно уравнение системы оставить без изменения, а другое уравнение системы заменить уравнением, ему равносильным, то полученная система будет равносильна заданной;
- Пусть дана система двух уравнений с двумя переменными. Если одно уравнение системы оставить без изменения, а другое уравнение заменить суммой или разностью обоих уравнений системы, то полученная система будет равносильна заданной.
Метод введения новых переменных применяется при решении систем двух уравнений с двумя переменными одним из следующих способов:
- Вводится одна новая переменная только для одного уравнения системы;
- Вводятся две новые переменные сразу для обоих уравнений.
Для того чтобы графически решить систему двух уравнений с двумя переменными, нужно в одной системе координат построить графики уравнений и найти координаты точек пересечения этих графиков.
Методы умножения и деления при решении систем уравнений основаны на следующем утверждении: если обе части уравнения 
ни при каких значениях 
одновременно не обращаются в нуль, то системы
5. Рациональные неравенства
Не нашли, что искали? Воспользуйтесь поиском: