Свойства производной

1. Постоянный множитель можно вынести за знак производной:

2. Производная алгебраической суммы функций равна алгебраической сумме производных этих функций

3. Производная произведения

4. Производная дроби (производная частного)

5. Производная сложной функции

Геометрический смысл производной. Производная в точке x ₀ равна угловому коэффициенту касательной к графику функции y = f (x) в этой точке.

11. Производные основных элементарных функций

Производные тригонометрических функций

Производную определим с помощью определения производной и I замечательного предела:

Производная выводится с помощью формул приведения и производной функции .

Производные могут быть определены как производные частного. К примеру,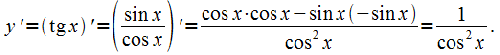

Производные обратных тригонометрических функций:

Основные правила дифференцирования.

Здесь мы выведем основные формулы, применяющиеся при нахождении производных - формулы для производных суммы, произведения, частного и т.д. Значение функции в точке х+Dx нам удобно будет представлять в виде у(х+Dx)= у(х)+ Dу= у(х)+ у'(x) Dх + a(Dх) Dх, где a(Dх) - БМ при Dх ®0, следующим из определения для приращения функции: Dу = у(х+Dx)- у(x).

Производная от обратно фунции

Пусть - дифференцируемая функция от аргумента x в некотором интервале . Если в уравнении y считать аргументом, а x - функцией, то возникает новая функция , где - функция обратная данной.

Не нашли, что искали? Воспользуйтесь поиском: