Тогда внутри отрезка существует по крайней мере одна такая точка

Тогда внутри отрезка существует по крайней мере одна такая точка

ε (a,b), в которой производная равна нулю (f′(ε)=0).

— Теорема Лагранжа. Пусть функция y=f(x) удовлетворяет следующим условиям:

непрерывна на [a,b];

дифференцируема на [a,b].

Тогда внутри отрезка существует по крайней мере одна такая точка

С(a,b), в которой производная равна частному от деления приращения функции к приращению аргумента на этом отрезке, т.е.

8. Непрерывность функции нескольких переменных.

Определение: Пусть точка М₀(х₀, у₀) принадлежит области определения функции f(x, y). Тогда функция z = f(x, y) называется непрерывной в точке М₀(х₀, у₀), если

(1)

причем точка М(х, у) стремится к точке М₀(х₀, у₀) произвольным образом.

Если в какой – либо точке условие (1) не выполняется, то эта точка называется точкой разрыва функции f(x, y). Это может быть в следующих случаях:

1) Функция z = f(x, y) не определена в точке М₀(х₀, у₀).

2) Не существует предел .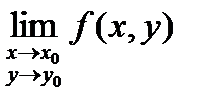

3) Этот предел существует, но он не равен f(x₀, y₀).

Свойства функций нескольких переменных, связанные

с их непрерывностью.

Свойство. Если функция f(x, y, …) определена и непрерывна в замкнутой и

ограниченной области D, то в этой области найдется по крайней мере одна точка

N(x₀, y₀, …), такая, что для остальных точек верно неравенство

f(x₀, y₀, …) ³ f(x, y, …)

а также точка N₁(x₀₁, y₀₁, …), такая, что для всех остальных точек верно неравенство

f(x₀₁, y₀₁, …) £ f(x, y, …)

тогда f(x₀, y₀, …) = M – наибольшее значение функции, а f(x₀₁, y₀₁, …) = m – наименьшее значение функции f(x, y, …) в области D.

Непрерывная функция в замкнутой и ограниченной области D достигает по крайней мере один раз наибольшего значения и один раз наименьшего.

Свойство. Если функция f(x, y, …) определена и непрерывна в замкнутой ограниченной области D, а M и m – соответственно наибольшее и наименьшее значения функции в этой области, то для любой точки m Î [m, M] существует точка

N₀(x₀, y₀, …) такая, что f(x₀, y₀, …) = m.

Проще говоря, непрерывная функция принимает в области D все промежуточные значения между M и m. Следствием этого свойства может служить заключение, что если числа M и m разных знаков, то в области D функция по крайней мере один раз обращается в ноль.

Свойство. Функция f(x, y, …), непрерывная в замкнутой ограниченной области D, ограничена в этой области, если существует такое число К, что для всех точек области верно неравенство .

Свойство. Если функция f(x, y, …) определена и непрерывна в замкнутой ограниченной области D, то она равномерно непрерывна в этой области, т.е. для любого положительного числа e существует такое число D > 0, что для любых двух точек (х₁, y₁) и (х₂, у₂) области, находящихся на расстоянии, меньшем D, выполнено неравенство

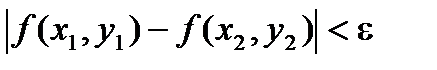
Приведенные выше свойства аналогичны свойствам функций одной переменной, непрерывных на отрезке. См. Свойства функций, непрерывных на отрезке.

Не нашли, что искали? Воспользуйтесь поиском: