Производные функций нескольких переменных.

Частная производная функция нескольких переменных по одной из этих переменных называется предел отношения частного приращения функции, приращению рассматриваемой независимой переменно, когда приращение стремится к нулю. Пусть – множество упорядоченных пар действительных чисел .
Определение 1. Если каждой упорядоченной паре чисел по некоторому закону 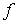поставлено в соответствие единственное действительное число , то говорят, что задана функция двух переменных 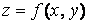или . Числа 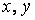называются при этом независимыми переменными или аргументами функции, а число – зависимой переменной.
Например, формула , выражающая объем цилиндра, является функцией двух переменных: – радиуса основания и – высоты.
Пару чисел иногда называют точкой , а функцию двух переменных – функцией точки .
Значение функции 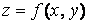в точке 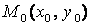обозначают или и называют частным значением функции двух переменных.
Совокупность всех точек , в которых определена функция 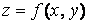, называется областью определения этой функции. Для функции двух переменных область определения представляет собой всю координатную плоскость или ее часть, ограниченную одной или несколькими линиями.
Например, область определения функции 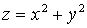– вся плоскость, а функции – единичный круг с центром в начале координат ( или .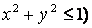

10 Определение: Полным дифференциалом функции z = f(x, y) называется главная линейная относительно Dх и Dу приращения функции Dz в точке (х, у).

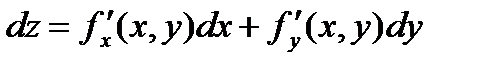
Для функции произвольного числа переменных:

Дифференциалом дифференцируемой в точке М(x₁,x₂,...,xп) функции Z=f (x₁,x₂,...,xп)

называется главная линейная относительно приращений аргументов часть приращения этой функции в точке М. Если все коэффициенты А в приращении функции в точке

независимой переменной можно понимать любое число. Договоримся в дальнейшем брать это число равным приращению независимой переменной.

11. поиск экстремума функции одной переменной.

1) 1.Найти производную функции

2) 2.Приравнять эту производную к нулю и решить уравнение. Корни этого уравнения будут критическими точками.

3) 3.Определить характер каждого критического значения аргумента, для этого, выясним меняет ли знак производная при переходе аргумента через данное критическое значение. Если меняется то критическая точка является экстремума, если нет, то у этой точки нет мах и мин.

Не нашли, что искали? Воспользуйтесь поиском: