Находим определитель исходной матрицы.

⇐ Предыдущая 2 3 4 5 678 9 10 11 Следующая ⇒

2.Если │А│=0, то матрица А вырожденная и обратной матрицы А^-1 не существует.

Если определитель матрицы А не равен нулю, то обратная матрица существует.

3. Находим А^T, транспонированную к А.

4. Находим алгебраические дополнения элементов транспонированной матрицы и составляем из них присоединенную матрицу. 5. Вычисляем обратную матрицу по формуле: 6. Проверяем правильность вычисления обратной матрицы, исходя из её определения А^-1∙А = А ∙А^-1 = Е.

26. N-мерное линейное векторное пространство

Векторное пространство R, называется n-мерным, если в нем существует n линейно независимых векторов, а любые n +1 векторов уже являются зависимыми.

Число n называется размерностью векторного пространство R и обозначается dim(R).

Совокупность n линейно независимых векторов n-мерного пространства R называется базисом.

Теорема. Каждый вектор Х векторного пространства R можно представить, и притом единственным способом, в виде линейной комбинации векторов базиса.

27. Системы векторов, операции над ними.

N-мерным вектором называется упорядоченная совокупность n действительных чисел, записываемых в виде Х =(х ₁, х ₂,… х _n), где х_i – i -я компонента вектора Х.

Два n-мерных вектора равны тогда и только тогда, когда равны их соответствующие компоненты, т.е. Х=У, если x_i=y_i, i=1…n.

Суммой двух векторов одинаковой размерности n называется вектор Z=X+Y, компоненты которого равны сумме соответствующих компонент слагаемых векторов, т.е. z_i=x_i+y_i, i=1…n.

Произведением вектора Х на действительное число λ называется вектор V=λX, компоненты которого равны произведению λ на соответствующие компоненты вектора Х, т.е. v_i=λx_i, i=1…n.

Линейные операции над векторами удовлетворяют следующим свойствам:

Х + У = У + Х;

(Х + У) + Z = X + (Y + Z);

a (bX) = (ab) X;

a (X + Y) = aX + aY;

(a + b) X = aX + bX;

Существует нулевой вектор О=(0,0,…0) такой, что Х + О = Х, для любого Х;

Для любого вектора Х существует противоположный вектор (- Х) такой, что Х + (- Х) = О;

1∙ Х = Х для любого Х.

Определение Множество векторов с действительными компонентами, в котором определены операции сложения векторов и умножения

· №28

· В матрице размера m x n вычеркиванием каких-либо строк и столбцов можно выделить квадратные подматрицы k-го порядка, где k≤min(m; n). Определители таких подматриц называются минорами k-го порядка матрицы А.

· Рангом матрицы А называется наивысший порядок отличных от нуля миноров этой матрицы.

· Ранг матрицы А обозначается rang A или r(A).

· Из определения следует:

· 1) ранг матрицы размера m x n не превосходит меньшего из её размеров, т.е. r(A) ≤ min (m; n).

· 2) r(A)=0 тогда и только тогда, когда все элементы матрицы равны нулю, т.е. А=0.

· 3) Для квадратной матрицы n-го порядка r(A) = n тогда и только тогда, когда матрица А – невырожденная.

· В общем случае определение ранга матрицы перебором всех миноров достаточно трудоемко. Для облегчения этой задачи используются элементарные преобразования, сохраняющие ранг матрицы:

· 1) Отбрасывание нулевой строки (столбца).

· 2) Умножение всех элементов строки (столбца) матрицы на число, не равное нулю.

· 3) Изменение порядка строк (столбцов) матрицы.

· 4) Прибавление к каждому элементу одной строки (столбца) соответствующих элементов другой строки (столбца), умноженных на любое число.

· 5) Транспонирование матрицы.

· Теорема. Ранг матрицы не изменится при элементарных преобразованиях матрицы.

№29

Линейные операторы

— Определение. Если задан закон (правило), по которому каждому вектору x пространства ставится в соответствие единственный вектор y пространства

то говорят: что задан оператор (преобразование, отображение) A(x), действующий из в и

записывают y=A(x).

— Оператор называется линейным, если для любого вектора x и y пространства

и любого числа λ выполняются следующие соотношения:

№31

— Пусть число уравнений системы (1) равно числу переменных, т.е. m=n. Тогда матрица системы является квадратной, а её определитель Δ=│А│называется определителем системы.

— Предположим, что │А│не равен нулю, тогда существует обратная матрица А^-1.

— Умножая слева обе части матричного равенства на обратную матрицу А^-1 получим:

— А^-1 (АХ)= А^-1 В.

Решением системы уравнений методом обратной матрицы будет матрица-столбец:

Х= А^-1В.

(А^-1 А)Х =ЕХ =Х

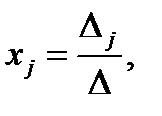
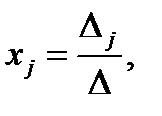— Теорема Крамера. Пусть Δ – определитель матрицы системы А, а Δ_j – определитель матрицы, полученный из матрицы заменой j-го столбца столбцом свободных членов. Тогда если Δ не равен нулю, то система имеет единственное решение, определённое по формулам Крамера:

где j=1..n.

⇐ Предыдущая 2 3 4 5 678 9 10 11 Следующая ⇒

Не нашли, что искали? Воспользуйтесь поиском:

vikidalka.ru - 2015-2025 год. Все права принадлежат их авторам! Нарушение авторских прав | Нарушение персональных данных