Теорема умножения. Если А и В независимые события, то

⇐ Предыдущая 4 5 6 7 8 9 101112 13 Следующая ⇒

Р(АВ) = Р(А)Р(В).

Если А и В совместны, то теорема сложения принимает вид:

Р(А+В)=Р(А)+Р(В) - Р(АВ).

Формула полной вероятности. Пусть событие А может наступить при условии реализации одной из гипотез Н₁, Н₂,..., Н_n, образующих полную группу событий. Тогда —. (1)

№41

Формула (1) называется формулой полной вероятности.

№42

— Предположим, что в результате испытания событие А произошло. Какова вероятность, что событие А произошло в результате реализации гипотезы Н_k, т.е. P(H_k/A) =? (происходит переоценка вероятностей гипотез). Ответ дает формула Байеса:

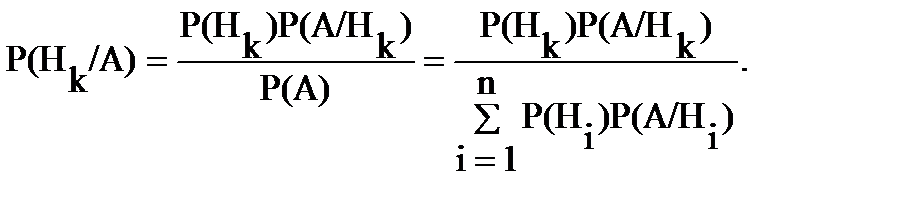
43. Формула Бернулли.

— Какова вероятность, что при n испытаниях coбытие А произойдет ровно k раз? (Обозначается P _n(k)). Ответ на этот вопрос дает формула Бернулли:

46.Основные числовые характеристики непрерывных случайных величин. — 1. Математическим ожиданием непрерывной случайной величины X с плотностью распределения j (х) называется число а = М(Х), определяемое равенством: — — 2. Дисперсией D(X) непрерывной случайной величины называется математическое ожидание квадрата отклонения случайной величины от её математического ожидания: — — D(Х) = М[Х-a]², а=M(X). Начальным моментом k-го порядка называется математическое ожидание k-ой степени случайной величины и обозначается: — — α_k=M(X^k). (M(X) = α₁= α). — — Центральным моментом k-го порядка называется математическое ожидание k-ой степени отклонения случайной величины от её математического ожидания и обозначается: — µ_k= M(X- M(X))^k. — — Из определения следует: µ₂= M(X- M(X))²=D(X). — Справедливы формулы: µ₀=1;µ₁=0;µ₂= α₂- α²; µ₃= α₃- 3αα₂+2α³; µ₄=α₄+6α²α₂-4αα₃-3α⁴. — Величина —

№44

Случайные величины, способы их описания. Случайной величиной называется переменная величина, которая в результате опыта может принимать то или иное значение. Случайная величина может быть дискретной или непрерывной. Будем обозначать случайные величины прописными буквами латинского алфавита X, Y, Z, а их значения - соответствующими строчными буквами х, у, z.

Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.

— Дисперсией D(X) случайной величины называется математическое ожидание квадрата ее отклонения от математического ожидания:

— D(X) = M[Х-M(X)]² или D(X) = M[X-a]², где а = М(Х). Часто вместо дисперсии используют среднее квадратическое отклонение:

— Свойства дисперсии случайной величины.

— 1. Дисперсия постоянной величины равна нулю: D(С) = 0.

— 2. Постоянный множитель можно выносить за знак дисперсии, возводя его и квадрат: D(кХ) = к²D(X)

— 3. Дисперсия случайной величины равна разности между математическим ожиданием квадрата случайной величины и квадратом математического ожидания D(X) = М(Х²)-[М(Х)]²

—

№45.

Основные числовые характеристики дискретных случайных величин. — Важнейшая из характеристик случайной величины ─ математическое ожидание: М(Х) = p₁x₁+ p₂x₂ + …+р_nх_n.

Математическим ожиданием (средним значением) М(Х) случайной дискретной величины называется сумма произведения всех ее значений на соответствующие им вероятности

№47

Дискретная случайная величина X имеет биномиальный закон распределения, если она принимает значения 0,1, 2,…,m,….,n с вероятностями р(m) = Р(Х = m) = C_n^m р^m qⁿ^-^m, где 0 < p <1, q = 1─ р.

— Биномиальный закон распределения представляет собой закон распределения числа Х = m наступлений события А в n независимых испытаниях, в каждом из которых оно может произойти с одной и той же вероятностью р.

⇐ Предыдущая 4 5 6 7 8 9 101112 13 Следующая ⇒

Не нашли, что искали? Воспользуйтесь поиском:

vikidalka.ru - 2015-2024 год. Все права принадлежат их авторам! Нарушение авторских прав | Нарушение персональных данных