Элементы комбинаторного анализа.

— Пустъ А – множество, состоящее из конечного числа элементов a ₁, a _2, a ₃… a_n. Из различных элементов множества А можно образовывать группы. Если в каждую группу входит одно и то же число элементов m (m из n), то говорят, что они образуют соединения из n элементов пo m в каждом. Различают три вида соединений: размещения, сочетания и перестановки.

— Соединения, в каждое из которых входят все n элементов множества А и которые, следовательно, отличаются друг от друга только порядком элементов называются перестановками из n элементов. Число таких перестановок обозначается символом Р_n.

— Tеорема 1. Число всех различных перестановок из n элементов равно Р_n = n (n − 1) (n − 2) (n − 3)…3 ∙ 2 ∙ 1 = 1 ∙ 2 ∙ 3…(n − 1) n = n!

— Соединения каждое из которых содержит m различных элементов (m < n) взятых из n элементов множества A, отличающихся друг oт друга или составом элементов, или их порядком называются размещениями из n элементов по m в каждом. Число таких размещений обозначается символом

— Tеорема 2. Число всех размещений из n элементов по m вычисляется по формуле:

— Иногда для записи числа размещений используют следующую формулу:

— Соединения каждое из которых содержит m различных элементов (m < n) взятых из n элементов множества А, отличающихся друг от друга по крайней мере одним из элементом (только составом) называются сочетаниями из n элементов по m в каждом. Число таких сочетаний обозначается символом

.

— Теорема 3. Число всех сочетаний из n элементов по m определяется формулой:

— Иногда для записи числа размещений используют следующую формулу:.

38. Непосредственный подсчет вероятности. — Из классического определения вероятности вытекают следующие ее свойства: — 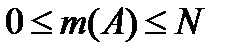Вероятность любого события заключена между нулем и единицей. — 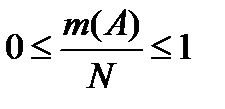Доказательство. Так как, то поделив все части неравенства на N, получим   — Откуда по классическому определению вероятности следует, что — Вероятность достоверного события равна единице. — Вероятность невозможного события равна нулю — Определение геометрической вероятности используется в задачах, когда общее и благоприятное число исходов бесконечно. Бросается наудачу точка в область G. Найти вероятность того, что точка попадет в область g. Вероятностьв этом случае будет вычисляться по формуле p=mera(g)/mera(G). mera(g) –площадь области g.

p=mera(g)/mera(G). mera(g) –площадь области g.

№39, 40

— Теорема сложения. Если А и В несовместны, то Р(А + В) = Р(А) +Р(В)