Аксиома полноты в форме Коши

Аксиома непрерывности (полноты). Каковы бы ни были непустые множества 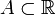и 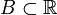, такие что для любых двух элементов и выполняется неравенство , существует такое число ξ, что для всех и имеет место соотношение .

Геометрически, если трактовать действительные числа как точки на прямой, данное утверждение представляется очевидным. Если два множества A и B таковы, что на числовой прямой все элементы одного из них лежат левее всех элементов второго, то найдется число ξ, разделяющее эти два множества, то есть лежащее правее всех элементов A (кроме, возможно, самого ξ) и левее всех элементов B (та же оговорка).

Здесь следует отметить, что несмотря на «очевидность» данного свойства, для рациональных чисел оно не всегда выполняется. Для примера, рассмотрим два множества:

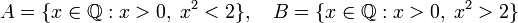
Легко видеть, что для любых элементов и выполняется неравенство a < b. Однако рационального числа ξ, разделяющего эти два множества, не существует. В самом деле, этим числом может быть только 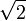, но оно не является рациональным.

31) Частные пределы последовательности. Теорема о существовании частного предела у ограниченной последовательности. Верхний и нижний пределы.

Не нашли, что искали? Воспользуйтесь поиском: