Классификация точек разрыва функции

Точка х₀ называется точкой разрыва функции f (x), если f (x) в точке х₀ не является непрерывной.

Это значит, что или не существует предела функции в данной точке, или этот предел не совпадает с тем значением, которое функция принимает в этой точке.

Точка х₀ называется точкой разрыва первого рода функции f(x), если в этой точке функция f(x) имеет конечные, но не равные друг другу правый и левый пределы

Точка х₀ называется точкой разрыва второго рода функции f(x), если в этой точке функция f (x) не имеет, по крайней мере, одного из односторонних пределов или хотя бы один из односторонних пределов бесконечен.

Так для функции в точке х = 0 односторонние пределы равны , то х = 0 является точкой разрыва второго рода.

36) Теорема о непрерывном образе замкнутого отрезка (теорема Вейерштрасса).

Фундаментальная теорема математического программирования, формулирующая условия существования глобального максимума. Заключается в том, что если допустимое множество X является компактным и непустым, то непрерывная целевая функция F(x), определенная на этом множестве, достигает глобального максимума на внутренней или граничной точке множества X.

При обобщении этой теоремы на случай бесконечномерного пространства можно получить основную теорему существования для задач управления. Согласно этой теореме, решение общей задачи управления существует, если целевой функционал является непрерывным функционалом от функций управления и если подмножество бесконечномерного пространства, к которому принадлежат управления, является компактным.

Формулировка.

Пусть дана непрерывная числовая функция, определённая на отрезке, то есть и . Пусть

— точные верхняя и нижняя грани множества значений функции f соответственно. Тогда эти значения конечны (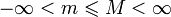) и достигаются (существуют такие, что ).

Замечания.

- По определению точки xm и xM являются точками глобального минимума и максимума соответственно. Таким образом непрерывная на отрезке функция достигает на нём своего минимума и максимума.

- В предположениях теоремы отрезок нельзя заменить на открытый интервал. Например, функция тангенс непрерывна в каждой точке области определения, но не ограничена.

- Иногда (в учебных курсах) два утверждения (об ограниченности и достижимости границ) разделяются на две теоремы Вейерштрасса - первую и вторую соответственно.

37) Производная, её геометрический и механический смысл. Односторонняя производная.

Произво́дная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если такой предел существует. Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке). Процесс вычисления производной называется дифференци́рованием. Обратный процесс — интегрирование.

Геометрический смысл производной состоит в том, что значение производной функции в точке равно угловому коэффициенту касательной к графику функции в этой точке. Для того, чтобы задать прямую y = kх + b, проходящую через данную точку А, достаточно указать ее угловой коэффициент. Угловой коэффициент прямой равен тангенсу угла α, образованному с осью абсцисс.

Механический смысл: производная по направлению характеризует скорость изменения функции в данном направлении. Если производная положительна – функция возрастает, если отрицательна – функция убывает.

Не нашли, что искали? Воспользуйтесь поиском: