Односторонняя производная

Правой (левой) производной функции f(x) в точке х = х₀ называется правое (левое) значение предела отношения при условии, что это отношение 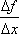существует.

Если функция f(x) имеет производную в некоторой точке х = х₀, то она имеет в этой точке односторонние производные. Однако, обратное утверждение неверно. Во- первых функция может иметь разрыв в точке х₀, а во- вторых, даже если функция непрерывна в точке х₀, она может быть в ней не дифференцируема.

38) Производные элементарных функций.

Найдем производные некоторых уже известных нам элементарных функций.

а) Тригонометрические функции.

По свойству предела произведения

(мы воспользовались первым замечательным пределом ). Итак,

Аналогичные рассуждения приводят к выводу, что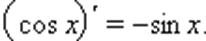

Производные тангенса и котангенса можно найти как производные частного:

б) Обратные тригонометрические функции.

Рассмотрим функцию y = arcsin x. На отрезке обратной к ней функцией будет x = sin y. Продифференцируем эту функцию по x, считая y функцией от x: или (на указанном отрезке). Аналогично выводятся формулы и для других обратных функций.

Получаем:

в) Степенная и показательная функции. Рассмотрим функцию y = a ^x. Для нее Но (это можно доказать, пользуясь определением числа e). Таким образом, если a > 0, a ≠ 1, то

Это и обуславливает частое использование основания e в математике и физике. В некоторых учебниках экспоненциальная функция даже вводится как функция, определенная на всей числовой оси, для которой f' (x) = f (x) и f (0) = 1.

Но 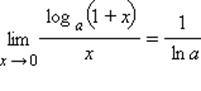(еще одно следствие замечательного предела ). Таким образом, если a > 0, a ≠ 1, то . В частности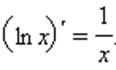

При x > 0 для любого Таким образом,

Не нашли, что искали? Воспользуйтесь поиском: