Верхний и нижний пределы

Нижний предел последовательности — это наименьший элемент множества частичных пределов последовательности.

Верхний предел последовательности — это наибольший элемент множества частичных пределов последовательности.

Иногда нижним пределом последовательности называют наименьшую из её предельных точек, а верхним — наибольшую. Очевидно, что эти определения эквивалентны.

Нижний предел последовательности :

- (в отечественной литературе);

Верхний предел последовательности :

- (в отечественной литературе).

32) Предел функции и его свойства.

Преде́л фу́нкции (предельное значение функции) в заданной точке, предельной для области определения функции, — такая величина, к которой стремится рассматриваемая функция при стремлении её аргумента к данной точке.

Предел функции является обобщением понятия предела последовательности: изначально, под пределом функции в точке понимали предел последовательности элементов области значений функции, составленной из образов точек последовательности элементов области определения функции, сходящейся к заданной точке (предел в которой рассматривается); если такой предел существует, то говорят, что функция сходится к указанному значению; если такого предела не существует, то говорят, что функция расходится.

Наиболее часто определение предела функции формулируют на языке окрестностей. То, что предел функции рассматривается только в точках, предельных для области определения функции, означает, что в каждой окрестности данной точки есть точки области определения; это позволяет говорить о стремлении аргумента функции (к данной точке). Но предельная точка области определения не обязана принадлежать самой области определения: например, можно рассматривать предел функции на концах открытого интервала, на котором определена функция (сами концы интервала в область определения не входят).

В общем случае необходимо точно указывать способ сходимости функции, для чего вводят т.н. базу подмножеств области определения функции, и тогда формулируют определение предела функции по (заданной) базе. В этом смысле система проколотых окрестностей данной точки — частный случай такой базы множеств.

Поскольку на расширенной вещественной прямой можно построить базу окрестностей бесконечно удалённой точки, то оказывается допустимым описание предела функции при стремлении аргумента к бесконечности, а, также, описание ситуации, когда функция сама стремится к бесконечности (в заданной точке). Предел последовательности (как предел функции натурального аргумента), как раз предоставляет пример сходимости по базе «стремление аргумента к бесконечности».

Отсутствие предела функции (в данной точке) означает, что для любого заранее заданного значения области значений и всякой его окрестности сколь угодно близко от заданной точки существуют точки, значение функции в которых окажется за пределами заданной окрестности.

Если в некоторой точке области определения функции существует предел и этот предел равен значению в данной функции, то функция оказывается непрерывной (в данной точке).

Свойства пределов:

- Одна и та же функция в одной и той же точке может иметь только один предел.

- Сходящаяся функция локально сохраняет знак.

- В частности, функция, сходящаяся к положительному (отрицательному) пределу, остаётся положительной (отрицательной) в некоторой окрестности предельной точки.

- Сходящаяся функция локально ограничена в окрестности предельной точки.

- Отделимость от нуля функций, имеющих предел, отличный от нуля.

- Операция взятия предела сохраняет нестрогие неравенства.

33) Некоторые важные пределы.

Если угол α выражен в радианах, то

Числом e называется предел

При нахождении многих пределов применяются следующие пределы

Частные случаи

При нахождении пределов вида необходимо иметь в виду следующее:

1) Если существуют конечные пределы

2) Если , то С находится с помощью формул

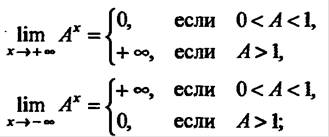
3) Если то, положив где

34) Сравнение бесконечно больших и бесконечно малых величин. Асимптотические разложения.

Бесконечно малая (величина) — числовая функция или последовательность, которая стремится к нулю.

Бесконечно большая (величина) — числовая функция или последовательность, которая стремится к бесконечности определённого знака.

Исчисление бесконечно малых — вычисления, производимые с бесконечно малыми величинами, при которых производный результат рассматривается как бесконечная сумма бесконечно малых.

Бесконечно малая величина.

Последовательность a_n называется бесконечно малой, если 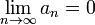. Например, последовательность чисел — бесконечно малая.

Функция называется бесконечно малой в окрестности точки x₀, если .

Функция называется бесконечно малой на бесконечности, если либо .

Также бесконечно малой является функция, представляющая собой разность функции и её предела, то есть если , то f(x) − a = α(x), .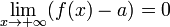

Бесконечно большая величина

Во всех приведённых ниже формулах бесконечность справа от равенства подразумевается определённого знака (либо «плюс», либо «минус»). То есть, например, функция xsin x, неограниченная с обеих сторон, не является бесконечно большой при .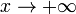

Последовательность a_n называется бесконечно большой, если .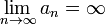

Функция называется бесконечно большой в окрестности точки x0, если .

Функция называется бесконечно большой на бесконечности, если 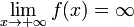либо .

Отношение бесконечно малых величин образует так называемую неопределённость .

Не нашли, что искали? Воспользуйтесь поиском: