Асимптотические разложения.

АСИМПТОТИЧЕСКОЕ РАЗЛОЖЕНИЕ - представление ф-ции f(x)в окрестности точки 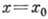в виде ряда (1),

где 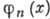, n = 0, 1, 2,... - последовательность ф-ций, для к-ро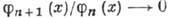й при (знак ~ означает асимптотич. равенство). Если коэффициенты -постоянные, то разложение (1) наз. асимптотич. разложением в смысле Пуанкаре, ряд в правой части (1) - асимптотич. рядом, а - выделенной точкой. Важным частным случаем асимптотич. рядов является асимптотич. степенной ряд

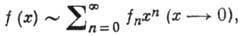(2) причём по определению

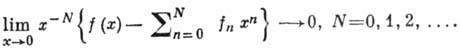(3)

Соответствующее ему А. р. есть А. р. в смысле Пуанкаре. Асимптотич. ряды, как правило, расходятся, тем не менее их практич. ценность очень велика, т. к. каждая частичная сумма ряда 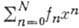даёт приближённое выражение для 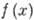с погрешностью, убывающей с уменьшением х тем быстрее, чем больше N. Однако, в отличие от сходящихся рядов, расходящиеся асимптотич. ряды могут обеспечить лишь нек-рую конечную точность приближения, зависящую от величины N. В квантовой теории поля, напр., асимптотич. ряд перенормированной теории возмущений по константе взаимодействия, точнее по её квадрату а, как правило, имеет факториально растущие коэфф., т. е. ряд имеет вид

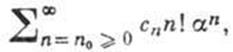(4)

где 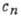- нек-рое медленно меняющееся по сравнению с 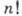число, 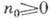зависит от представляемой рядом величины. В частности, в квантовой электродинамике, где 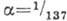, несмотря на расходимость ряда (4), его частичные суммы, вплоть до N= 137, обеспечивают точность приближения, к-рая практически может считаться абсолютной.

35) Непрерывные функции. Классификация точек разрыва функции.

Непрерывная функция — функция без «скачков», то есть такая у которой малые изменения аргумента приводят к малым изменениям значения отображения. График непрерывной функции может быть начерчен «не отрывая карандаш от бумаги».

Непрерывная функция вообще говоря, — синоним понятия непрерывное отображение, тем не менее, чаще всего этот термин используется в более узком смысле — для отображений между числовыми пространствами, например, на вещественной прямой.

Пусть 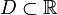и .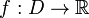

Функция f непрерывна в точке 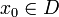, если для любого 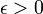существует δ > 0 такое, что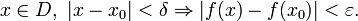

Функция f непрерывна на множестве E, если она непрерывна в каждой точке данного множества.

В этом случае говорят, что функция f класса C⁰ и пишут: 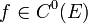или, подробнее, .

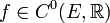Из определения следует, что функция непрерывна в каждой изолированной точке своей области определения.

Определение непрерывности фактически повторяет определение предела функции в данной точке. Другими словами, функция f непрерывна в точке x₀, предельной для множества E, если f имеет предел в точке x₀, и этот предел совпадает со значением функции f(x₀).

Функция непрерывна в точке, если её колебание в данной точке равно нулю.

Не нашли, что искали? Воспользуйтесь поиском: