
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Вывод нестационарного уравнения нестационарного распределения температуры в грунте.
7.1. Постановка задачи
Подогретый до температуры θ1 (град.) нефть перевозится по подземному трубопроводу.
Глубина прокладки нефтепровода Н(м).
Считая, что теплоотдача происходит только по вертикальному направлению определить распределение температуры от трубы до поверхности земли.

Ось ОХ направим вертикально вверх (рис. 1). На оси ОХ выделим элемент с координатами х и х + Δх. Тогда приращение энергии в направлений оси х за время Δt будет
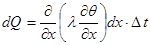 (7.1)
(7.1)
С другой стороны, согласно закону сохранения энергий,
 (7.2)
(7.2)
Левые части (7.1) и (7.2) равны, поэтому
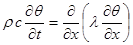
где ρ– плотность грунта [кг/м3];
с – массовая теплоемкость грунта [кдж/кг.град];
λ – коэффициент теплопроводности грунта [вт/м•град.].
При х = 0 задается температура. На поверхности земли происходит конвективный теплообмен между поверхностью тела и окружающей средой (воздух).
В основу изучения конвективного теплообмена положен закон Ньютона-Рихмана

где q – плотность теплового потока, вт/м2;
θ0 – температура воздуха, 0С;
θгр – температура поверхности грунта,0С;
α – коэффициент теплоотдачи, вт/(м2•град);
Согласно закону сохранения энергии, количество теплоты, отдаваемый единицей поверхности тела окружающей среде за единицу времени вследствие теплоотдачи, должно быть равно теплоте, которая путем теплопроводности подводится к единице поверхности в единицу времени со стороны внутренних частей тела, т.е.
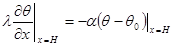 (7.3)
(7.3)
Равенство (7.3) является математической формулировкой граничного условия третьего рода; оно является действительной для каждого момента времени t.
называется граничным условием первого рода.
Получена задача: найти решение нестационарного параболического уравнения со смешанными граничными условиями, т.е. 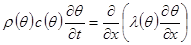 (7.4)
(7.4)
θ(t,0) = θ1 = const (7.5)
 (7.6)
(7.6)
 (7.7)
(7.7)
Теорема 1. При определенных условиях на ρ(θ), с(θ) и λ(θ) задача (7.4) - (7.7) имеет единственное решение.
Приближенный метод решения задачи (7.4) – (7.6).
Решение задачи (7.4) – (7.6) зависит от двух переменных 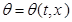 , где t – время, час; х – координата точки грунта, м. Поэтому задача (7.4) – (7.6) решается в области Q= (0, Тmax)•(0,H),
, где t – время, час; х – координата точки грунта, м. Поэтому задача (7.4) – (7.6) решается в области Q= (0, Тmax)•(0,H), 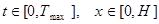
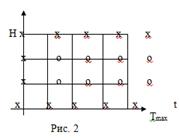
Сетка. Отрезок [0, H] разбиваем на N равных частей с шагом h = H/N, а отрезок [0, Tmax] на М равных частей с шагом ∆t = Tmax /M. Тогда получается сетка (рис. 2). 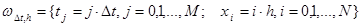
В рис.2 «крестиками» - х обозначены граничные узлы, а «ноликами» - 0 обозначены внутренние узлы.
Аппроксимация выражений
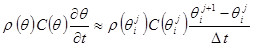
т.е. функций ρ(θ) и с(θ) определяются на нижних слоях. В начальный момент времени, т.е. при
 .
.
Вместо задачи (7.4) – (7.7) решается приближенная задача
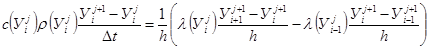 (7.8)
(7.8)
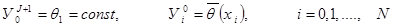 (7.9)
(7.9)
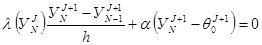 (7.10)
(7.10)
В системе (7.8) i = 1, 2, …, N-1 при каждом j=0,1,…,M-1.
Систему линейных алгебраических уравнений перепишем в виде
 (7.11)
(7.11)
i = 1, 2, …, N-1 при каждом j=0,1,…,M-1.
Где
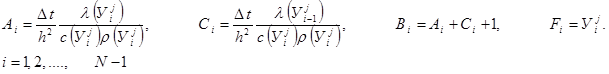
2 вариант
Не нашли, что искали? Воспользуйтесь поиском: