Понятие разбиения множества на классы

Понятия множества и операций над множествами позволяют уточнить наше представление о классификации - действии распределения объектов по классам.

Классификацию мы выполняем достаточно часто. Так, натуральные числа представляем как два класса - четные и нечетные. Углы на плоскости разбиваем на три класса: прямые, острые и тупые.

Любая классификация связана с разбиением некоторого множества объектов на подмножества. При этом считают, что множество X разбито на классы X₁, Х₂,..., Х_n..., если:

1) подмножества Х₁, Х₂,..., Х_п,... попарно не пересекаются; |

2) объединение подмножеств X₁, Х₂,..., Х_n,... совпадает с множеством X. |

Если не выполнено хотя бы одно из условий, классификацию считают неправильной. Например, если из множества X треугольников выделить подмножества равнобедренных, равно-сторонних и разносторонних треугольников, то разбиения мы не получим, поскольку подмно-жества равнобедренных и равносторонних треугольников пересекаются (все равносторонние треугольники являются равнобедренными). В данном случае не выполнено первое условие разбиения множества на классы.

Так как разбиение множества на классы связано с выделением его подмножеств, то классификацию можно выполнять при помощи свойств элементов множеств.

Рассмотрим, например, множество натуральных чисел. Его элементы обладают различными свойствами. Положим, что нас интересуют числа, обладающие свойством «быть кратным 3». Это свойство позволяет выделить из множества натуральных чисел подмножество, состоящее из чисел, кратных 3. Тогда про остальные натуральные числа можно сказать, что они не кратны 3, т.е. получаем еще одно подмножество

множества натуральных чисел (рис. 12). Так как выделенные подмножества не пересекаются, а их объединение совпадает с множеством натуральных чисел, то имеем разбиение этого множества на два класса.

Рис. 12	Рис. 13

Вообще, если на множестве X задано одно свойство, то это множество разбивается на два класса. Первый - это класс объектов, обладающих этим свойством, а второй - дополнение первого класса до множества X. Во втором классе содержатся такие объекты множества X, которые заданным свойством не обладают. Такую классификацию называют дихотомической.

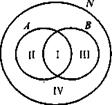
Рассмотрим теперь ситуацию, когда для элементов множества заданы два свойства. Например, такие свойства натуральных чисел, как «быть кратным 3» и «быть кратным 5». При помощи этих свойств из множества N натуральных чисел можно выделить два подмножества: А - подмножество чисел, кратных 3, и В - подмножество чисел, кратных 5. Эти множества пересекаются, но ни одно из них не является подмножеством другого (рис. 13). Проанализируем получившийся рисунок. Конечно, разбиения множества натуральных чисел на подмножества А и В не произошло. Но круг, изображающий множество N, можно рассматривать как состоящий из четырех непересекающихся областей - на рисунке они пронумерованы. Каждая область изображает некоторое подмножество множества N. Подмножество I состоит из чисел, кратных 3 и 5; подмножество II - из чисел, кратных 3 и не кратных 5; подмножество III - из чисел, кратных 5 и не кратных 3; подмножество IV - из чисел, не кратных 3 и не кратных 5. Объединение этих четырех подмножеств есть множество N.

Не следует думать, что задание двух свойств элементов множества всегда приводит к разбиению этого множества на четыре класса. Например, при помощи таких двух свойств «быть кратным 3» и «быть кратным 6» множество натуральных чисел разбивается на три класса (рис. 14): I -класс чисел, кратных 6; II - класс чисел, кратных 3, но не кратных 6; III - класс чисел, не кратных 3.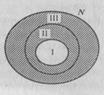

Рис. 14

Таким образом, выделение двух свойств привело к разбиению множества N натуральных чисел на четыре класса.

Упражнения

1. Из множества X = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12} выделили подмножества X,, Х₂ и Х₃. В каком из следующих случаев множество Х оказалось разбитым на классы:

а) Х₁ = {1, 3, 5, 7, 11}, Х₂ = {2, 4, 6, 8, 10, 12}, Х₃ = {9};

б) Х₁ = {1,3,5,7,9,11}, Х₁ = {2,4,6,8, 10,12}, Х ₁= {10, 11,12};

в) Х₁ = {3,6, 9, 12}, Х₂= {1,5,7, 11},Х₃= {2, 10}?

2. Из множества Х= {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12} выделим подмножества:

а) А - четных чисел, В - нечетных чисел;

б) А - чисел, кратных 2; В - чисел, кратных 3; С- чисел, кратных 4;

в) А - нечетных однозначных чисел; В - четных двузначных чисел. В каком случае произошло разбиение множества Х на классы?

3. Из множества треугольников выделили подмножества треугольников:

а) прямоугольные, равнобедренные, равносторонние;

б) остроугольные, тупоугольные, прямоугольные;

в) равносторонние, прямоугольные, тупоугольные.

В каком случае произошло разбиение множества треугольников на классы?

4.На какие классы разбивается множество точек плоскости при помощи:

а) окружности;

б) круга;

в) прямой?

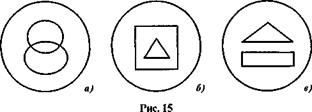
5.Перечертите комбинации фигур, приведенные на рисунке 15, и на каждой из них выделите (различными видами штриховки) непересекающиеся области.

6. На множестве натуральных чисел рассматривается свойство «быть кратным 7». Сколько классов разбиения множества N оно определяет? Назовите по два элемента из каждого класса.

7. Из множества четырехугольников выделили подмножество фигур с попарно параллельными сторонами. На какие классы разбивается множество четырехугольников с помощью свойства «иметь попарно параллельные стороны»? Начертите по два четырехугольника из каждого класса.

8. Изобразите при помощи кругов Эйлера множество N натуральных чисел и его подмножества: четных чисел и чисел, кратных 7. Можно ли утверждать, что множество N разбито:

а) на два класса: четных чисел и чисел, кратных 7;

б) на четыре класса: четных чисел, кратных 7; четных чисел, не кратных 7; нечетных чисел, кратных 7; нечетных чисел, не кратных 7?

9. На множестве четырехугольников рассматриваются два свойства: «быть прямоугольником» и «быть квадратом». На какие классы разобьется множество четырехугольников при помощи этих свойств? Начертите по два четырехугольника из каждого класса.

10. Изменится ли ответ в упражнении 9, если на множестве четырехугольников рассмотреть свойства:

а) «быть прямоугольником» и «быть ромбом»;

б) «быть прямоугольником» и «быть трапецией»?

11. На рисунке 16 изображены множество X- студентов группы, А - множество спортсменов этой группы, В - множество отличников этой группы. а) Укажите классы разбиения множества X, полученные с помощью свойств «быть спортсменом» и «быть отличником», и охарактеризуйте каждый из них. б) Сколько получилось бы классов разбиения, если бы ни один отличник группы не был спортсменом?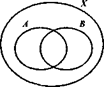

Рис 16

11. На рисунке 16 изображены множество X- студентов группы, А - множество спортсменов этой группы, В - множество отличников этой группы.

а) Укажите классы разбиения множества X, полученные с помощью свойств «быть спортсменом» и «быть отличником», и охарактеризуйте каждый из них.

б) Сколько получилось бы классов разбиения, если бы ни один отличник группы не был спортсменом?

Выполните соответствующий рисунок и назовите классы разбиения.

12. Покажите, что решение нижеприведенных задач связано с разбиением заданного множества на классы:

а) 18 редисок связали в пучки по 6 редисок в каждом. Сколько получилось пучков?

б) 18 карандашей раздали 6 ученикам поровну. Сколько карандашей у каждого?

13. О каких множествах и операциях над ними идет речь в задачах:

а) С одной грядки сняли 25 кочанов капусты, а с другой - 15 кочанов. Всю эту капусту разложили в корзины, по 8 кочанов в каждую. Сколько потребовалось корзин?

б) Для школьного сада привезли 24 саженца яблонь. На одном участке посадили 6 саженцев, а на другом - остальные, в 3 ряда поровну. Сколько саженцев посадили в каждом ряду?

Не нашли, что искали? Воспользуйтесь поиском: