Число элементов в объединении и разности конечных множеств

Нам известно, как находят объединение двух конечных непересекающихся множеств. Например, если А = {х, у, z}, а В = {k, l, т, р}, то А È В - {х, у, z, k, l, т, р}. Чтобы ответить на вопрос: «Сколько элементов в полученном множестве?», достаточно пересчитать их.

А как определять число элементов в объединении конечных множеств, не образуя его и не обращаясь к пересчету элементов?

Условимся предложение «Множество А содержит а элементов» записывать в таком виде: п(А) = а. Например, если А = {х, у, z}, то утверждение «Множество А содержит три элемента» можно записать так: п (А) = 3.

Можно доказать, что если в множестве А содержится а элементов, а в множестве В-b элементов и множества А и В не пересекаются, то в объединении множеств А и В содержится а + b элементов, т.е.

n(АÈВ)=п(А)+п{В)=а + b. (1)

Это правило нахождения числа элементов в объединении двух конечных непересекающихся множеств, его можно обобщить на случай t попарно непересекающихся множеств, т.е. если множества А₁ А₂,..., А_t, попарно не пересекаются, то п{А₁ È А₂ È... и А,) = = п(А₁) + п(А₂) +... + п(А₁).

Пусть, например, А = {х, у, z.}, В - {k, l, т, р},С= { q, s }. Найдем число элементов в объединении данных множеств.

Пересчитав элементы данных множеств, получаем, что п(А) = 3, п(В) = 4, n (С) = 2. Видим, что А Ç В = Æ, А Ç С = Æ, В Ç С = Æ, т.е. данные множества попарно не пересекаются. Тогда, согласно правилу нахождения числа элементов в объединении конечных множеств, получаем:

п(А È В ÈС) = п(А) + п(В) + п(С) = 3 + 4 + 2 = 9.

Таким образом, в объединении заданных трех множеств содержится 9 элементов.

Нетрудно убедиться в том, что если В Ì А, то п(В¢_А) = п(А) - п(В), т.е. число элементов дополнения подмножества В до данного конечного множества А равно разности численностей этих множеств.

Пусть, например, А = {х, у, z, р, t}, а В = {х, р, t}. Найдем число элементов в дополнении подмножества В до множества А.

Пересчитав элементы множеств А и В, получаем, что п(А) = 5, п(B) = 3. Тогда

п(В'_А) = п(А) - п(В) = 5 - 3 = 2. Таким образом, в дополнении множества В до множества А содержится два элемента.

Формула (1) позволяет находить число элементов в объединении конечных непересекающихся множеств. А если множества А и В имеют общие элементы, то как найти число элементов в их объединении?

Пусть, например, А = {х, у, z}, а В = {х, z, р, s, k}. Тогда А È В = {х, у, z, р, s, k}, т.е. если (A) = 3, а п(В) = 5 и А Ç В ¹Æ, то п(А È В) = 6. Нетрудно видеть, что в данном случае п(А Ç В) = 2 и, значит, общие элементы множеств А и В в объединении этих множеств записаны только один раз.

В общем виде правило подсчета элементов в объединении двух конечных множеств может быть представлено в виде формулы:

п(АÈВ) = п(А)+п(В)-п(АÇВ). (2)

Полученные формулы для подсчета числа элементов в объединении двух и более множеств можно использовать для решения текстовых задач следующего вида.

Задача 1. Из 40 студентов курса 32 изучают английский язык, 21 -немецкий язык, а 15 - английский и немецкий языки. Сколько студентов курса не изучает ни английский, ни немецкий языки?

Решение. Пусть А - множество студентов курса, изучающих английский язык, В - множество студентов курса, изучающих немецкий язык, С- множество всех студентов курса. По условию задачи: п(А) = 32, п(В) = 21, п(АÇВ) = 15, п(С) = 40. Требуется найти число студентов курса, не изучающих ни английского, ни немецкого языка.

1 способ.

1) Найдем число элементов в объединении данных множеств А и В.
Для этого воспользуемся формулой (2):

п(АÈВ) = п(А) + п(B) - п(А Ç В) = 32 + 21 - 15 = 38.

2) Найдем число студентов курса, которые не изучают ни английский, ни немецкий языки: 40 - 38 = 2.

1) Изобразим данные множества при помощи кругов Эйлера и определим число элементов в

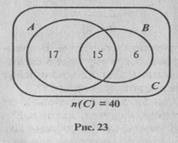
каждом из непересекающихся подмножеств (рис. 23). Так как в пересечении множеств А и В содержится 15 элементов, то студентов, изучающих только английский язык, будет 17 (32 - 15 = 17), а студентов, изучающих только немецкий, -6(21 -15 = 6). Тогда п(AÈB) = 17 + 15 + 6 = 38, и, следовательно, число студентов курса, которые не изучают ни английский, ни немецкий языки, будет 40 - 38 = 2.

Упражнения

1. Из 32 школьников 12 занимаются в волейбольной секции, 15 - в баскетбольной, 8 человек занимаются и в той, и в другой секции.

Сколько школьников не занимаются ни в волейбольной, ни в баскетбольной секции?

2. В третьем классе дети коллекционируют марки и монеты. Марки коллекционируют 8 человек, монеты - 5 человек. Всего коллекционеров 11. Объясните, как это может быть. Сколько человек коллекционируют только марки?... только монеты?

3. Из 38 учащихся класса 24 занимаются в хоре и 15 в лыжной секции. Сколько учащихся занимается и в хоре, и в лыжной секции, если в классе нет учащихся, не посещающих занятий хора или лыжной секции?

4. В группе туристов, состоящей из 100 человек, 10 человек не знали ни немецкий, ни французский языки, 75 знали немецкий, 83 знали французский. Сколько туристов знали два языка?

5. Катя положила в коробку 4 зеленых круга, 6 треугольников и 3 красных многоугольника. Всего в коробке оказалось 11 фигурок. Сколько среди них красных треугольников?

6. В делегации 6 человек, знающих французский или немецкий язык. Трое из них говорят только на французском, двое - только на немецком. Сколько человек говорят на двух языках - французском и немецком?

7.Правильно ли представлено на рисунке 24 условие следующей задачи: «Из 100 человек английский язык изучают 28, немецкий - 30, французский - 42, английский и немецкий -8, английский и французский - 10, немецкий и французский - 5. Все три языка изучают три студента. Сколько студентов изучает только один язык? Сколько студентов не изучает ни одного языка?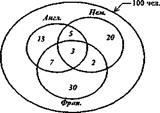

Рис.24

8. Решите задачу из задания 7.

9. В школе 70 учеников. Из них 27 ходит в драмкружок, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов. 3 спортсмена посещают и драмкружок, и хор. Сколько ребят не поют в хоре, не увлекаются спортом и не ходят в драмкружок?

10. Даны 40 чисел. Из них 10 чисел кратны 3, 15 чисел кратны 2, 20 чисел не кратны ни 2, ни 3. Сколько среди данных 40 чисел, кратных 6?

11. На уроке литературы учитель решил узнать, кто из 40 учеников класса читал книги А, В и С. Результаты опроса оказались таковы: книгу А читали 25 учащихся, книгу В - 22, книгу С - также 22. Книгу А или В читали 33 ученика, А или С - 32, В или С - 31; все три книги прочли 10 учащихся. Сколько учеников прочли только по одной книге. Сколько учащихся не читали ни одной из этих трех книг?

Не нашли, что искали? Воспользуйтесь поиском: