Декартово произведение множеств

Используя две цифры, например, 3 и 5, можно записать четыре Двузначных числа: 35, 53, 33 и 55. Несмотря на то, что числа 35 и 53 записаны с помощью одних и тех же цифр, эти числа

различные. В том случае, когда важен порядок следования элементов, в математике говорят об упорядоченных наборах элементов. В рассмотренном примере мы имели дело с упорядоченными парами.

Упорядоченную пару, образованную из элементов а и b, принято записывать, используя круглые скобки: (а;b). Элемент а называют первой координатой (компонентой) пары, а элемент b - второй координатой (компонентой) пары.

Пары (а;b) и (с;d) равны в том и только в том случае, когда а = с и b=d.

В упорядоченной паре (а;b) может быть, что а =b. Так, запись чисел 33 и 55 можно рассматривать как упорядоченные пары (3; 3) и (5; 5).

Упорядоченные пары можно образовывать как из элементов одного множества, так и двух множеств. Пусть, например, А = {1, 2, 3}, В = {3, 5}. Образуем упорядоченные пары так, чтобы первая компо­нента принадлежала множеству А, а вторая - множеству В. Если мы перечислим все такие пары, то получим множество:

{(1;3),(1;5),(2;3),(2;5),(3;3),(3;5)}.

Видим, что имея два множества А и В, мы получили новое множество, элементами которого являются упорядоченные пары чисел. Это множество называют декартовым произведением множеств А и В.

Определение. Декартовым произведением множеств АиВназывается множество всех пар, первая компонента которых принадлежит множеству А, а вторая компонента принадлежит множеству В.

Декартово произведение множеств А и В обозначают А ´ В. Используя это обозначение, определение декартова произведения можно записать так:

А ´ В- {(х;у) | хÎ А и уÎ В}.

Задача 1. Найдите декартово произведение множеств А и В, если:

а) А = {т; р}, В ={e,.f;k}

б) А=В={3,5}.

Решение, а) Действуем согласно определению - образуем все пары, первая компонента которых выбирается из А, а вторая - из В:

А ´ В = {(т; е), (m; f), (т; к), (р; е), (р; f) (р; к)}.

б) Декартово произведение равных множеств находят, образуя всевозможные пары из элементов данного множества:

А ´ А = {(3;3),(3;5),(5;3),(5;5)}.

Выясним, какими свойствами обладает операция нахождения декартова произведения. Так как декартовы произведения А ´ В и В ´ А состоят из различных элементов, то операция нахождения декартова произведения множеств свойством коммутативности не обладает.

Аналогично рассуждая, можно доказать, что для этой операции не выполняется и свойство ассоциативности. Но она дистрибутивна относительно объединения и вычитания множеств, т.е. для любых множеств А, В и С выполняются равенства:

(А È В) ´ С - (А ´С) È (В ´ С),

(А\В) ´ С = (А ´ С)\(В ´ С).

Задача 2. Проверьте справедливость свойства дистрибутивности декартова произведения относительно объединения, если:

А = {3; 4; 5}, В ={5; 7}, С ={7; 8}.

Решение. Найдем объединение множеств А и В: А È В = {3, 4, 5, 7}. Далее перечислим элементы множества (А È В) ´С, используя определение декартова произведения: (А È В) ´ С ={(3; 7), (3; 8), (4; 7), (4; 8), (5; 7), (5; 8), (7; 7), (7; 8)}.

Чтобы найти элементы множества (А ´ С) È (В ´ С), перечислим сначала элементы множеств А ´ С и В ´ С:

А ´ С= {(3; 7), (3; 8), (4; 7), (4; 8), (5; 7), (5; 8)}

В ´ С= {(5; 7), (5; 8), (7; 7), (7; 8)}.

Найдем объединение полученных декартовых произведений:

(А ´ С) È (В ´ С) = {(3; 7), (3; 8), (4; 7), (4; 8),

(5; 7), (5; 8), (7; 7), (7; 8)}.

Видим, что множества (А È В) ´С и (А ´С) È (В ´С) состоят из одних и тех же элементов, следовательно, для данных множеств А, В и С справедливо равенство (А È В) ´С = (А ´С) È (В ´С).

Выясним теперь, как можно наглядно представлять декартово произведение множеств.

Если множества А и В конечны и содержат небольшое число элементов, то можно изобразить декартово произведение этих множеств при помощи графа или таблицы. Например, декартово произведение множеств А = {1, 2, 3} и В = {3, 5} можно представить так, как показано на рисунке 17, а, б.

Декартово произведение двух числовых множеств (конечных и бесконечных) можно изображать на координатной плоскости, так как каждая пара чисел может быть единственным образом изображена точкой на этой плоскости. Например, декартово произведение А ´ В множеств А = {1, 2, 3} и В = {3, 5} на координатной плоскости будет выглядеть так, как показано на рисунке 18.

Заметим, что элементы множества А мы изобразили на оси Ох, а элементы множества В - на оси Оу. Такой способ наглядного представления декартова произведения двух числовых множеств удобно использовать в случае, когда хотя бы одно из них бесконечное.

Задача 3. Изобразите на координатной плоскости декартово произведение А ´ В, если:

а) А = {1, 2, 3}, В = [3, 5]; б) А = [1, 3], В = [3, 5];

в) А = R ., В = [3,5]; г) А = R, В = R.

Решение. а) Так как множество А состоит из трех элементов, а множество В содержит все действительные числа от 3 до 5, включая и сами эти числа, то декартово произведение А ´В

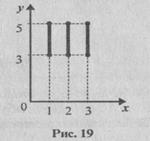
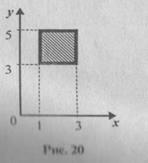
будет состоять из бесконечного множества пар, первая компонента которых либо 1, либо 2, либо 3, а вторая - любое действительное число из промежутка [3, 5]. Такое множество пар действительных чисел на координатной плоскости изобразится тремя отрезками (рис. 19). б) В этом случае бесконечны оба множества А и В. Поэтому первой координатой пары, принадлежащей множеству А ´ В, может быть любое число из промежутка [1, 3], и, следовательно, точки, изображающие элементы декартова произведения данных множеств А и В, образуют квадрат (рис. 20).

Чтобы подчеркнуть, что элементы декартова произведения изображаются и точками, лежащими

внутри квадрата, этот квадрат можно заштриховать.

	в) Этот случай отличается от предыдущего тем, что множество А состоит из всех действительных чисел, т.е. абсцисса точек, изображающих элементы множества А ´ В, принимает все действительные значения, в то время как ордината выбирается из промежутка [3, 5]. Множество таких точек образует полосу (рис. 21).
г) Декартово произведение R ´ R состоит из всевозможных действительных чисел. Точки, изображающие эти пары, сплошь заполняют координатную плоскость. Таким образом, декартово произведение R ´ R содержит столько же элементов, сколько точек находится на координатной плоскости. В математике и других науках рассматривают не только упорядоченные пары, но и упорядоченные наборы из трех, четырех и т.д. элементов. Например, запись числа 367 - это упорядоченный набор из трех элементов, а запись слова «математика» - это упорядоченный набор из 10 элементов.	Рис. 21

Упорядоченные наборы часто называют кортежами и различают по длине. Длина кортежа - это число элементов, из которых он состоит. Например, (3; 6; 7) - это кортеж длины 3, (м, а, т, е, м, а, т, и, к, а) - это кортеж длины 10.

Рассматривают в математике и декартово произведение трех, четырех и вообще п множеств.

Определение. Декартовым произведением множеств А1, А2,..., Апназывается множество всех кортежей длинып, первая компонента которых принадлежит множеству А1, вторая - множеству А2,..., п-я - множеству Ап.

Декартово произведение множеств А,, А₂,..., А„ обозначают так: А,´А₂´...´А„.

Задача 4. Даны множества: А₁ = {2, 3} ,А₂ = {3, 4, 5}, А₃ = {6, 7}. Найти А₁ ´А₂ ´А₃.

Решение. Элементами множества А₁ ´ А₂ ´ А₃ будут кортежи длины 3 такие, что первая их компонента принадлежит множеству А₁, вторая - множеству А₂, третья - множеству А₃. А₁ ´А₂´А₃ = {(2, 3, 6), (2, 3, 7), (2, 4, 6), (2, 4, 7),

(2, 5, 6), (2, 5, 7), (3, 3, 6), (3, 3, 7),

(3,4, 6), (3,4, 7), (3,5, 6), (3,5, 7)}.

Упражнения

1. Дано уравнение 2х - 3 = у. Запишите несколько решений данного уравнения. Что предоставляет собой каждое решение? Является ли пара (4, 5) решением данного уравнения? А пара (5, 4)?

2. Элементами множеств А и В являются пары чисел:

А = {(1,12), (2, 9), (3,6), (4,3), (5,0)},

В = {(1,9), (2, 7), (3,6), (4, 7), (5,0)}.

Найдите пересечение и объединение данных множеств.

3. Перечислите элементы декартова произведения А ´ В, если:

а)А = {а,b,с,d),В= {b, к, l };

б) А =В= {а,b,с}

в)А = {а,b,с},В = Æ.

4. Запишите различные двузначные числа, используя цифры 3, 4 и 5. Сколько среди них таких, запись которых начинается с цифры 3? Как связано решение данной задачи с понятием декартова произведения множеств?

5. Даны два множества: А = {1, 3, 5} и В = {2, 4}. Перечислите элементы множеств А´ В и В´А. Верно ли, что:

а) Множества А´В и В´А содержат одинаковое число элементов;

б) Множества А ´ В и В ´ А равны?

6. Проверьте справедливость равенства (А È В) ´ С - (А ´ С) È (В ´ С)
для множестве = {3, 5,7}, В = {7,9}, С = {0, 1}.

Выполняется ли для них равенство (А \ В) ´ С = (А´С) \ (В ´ С)?

7. Сколько букв в слове «барабан»? Сколько различных букв в этом слове?

Сформулируйте эту задачу, используя понятия множества и кортежа.

8. Чем отличается множество цифр в записи числа 56 576 от кортежа цифр в его записи?

9. Изобразите на координатной плоскости точки: (-1, 0), (-1, 4), (3, 0), (3, 4) и последовательно их соедините. Какая фигура получилась?

10. Какую фигуру образуют точки, если их абсциссы принадлежат множеству [-2, 2], а ординаты - множеству [-3, 3]?

11. Изобразите в прямоугольной системе координат множество А´ В, если:

а) А = [-2, 2], B = {2,3,4};

б) А = [-2, 2], В = (2, 4);

в) А = R, В = [2, 4].

12. Определите, декартово произведение каких множеств X и Y изображено на рисунке 22.

Не нашли, что искали? Воспользуйтесь поиском: