Отношения между множествами

Вматематике изучают не только те или иные множества, нои отношения, взаимосвязи между ними. Например, нам известно, что все натуральные числа являются целыми. Понятие множества позволяет обобщить конкретные случаи взаимосвязи между различными совокупностями, позволяет посмотреть на них с единой точки зрения.

Если множества А и В имеют общие элементы, т.е. элементы, принадлежащие одновременно А и В, то говорят, что эти множества пересекаются.

Например, если А = {а, b, с, d, е), В = {b, d, к, т), С = {х, у, z}, то можно утверждать, что множества А и В пересекаются, так как имеют общие элементы b и d, а множества А и С, В и С не пересекаются, поскольку не имеют общих элементов.

Рассмотрим теперь множества А = {а, b, с, d, е} и В = {с, d, е}. Они пересекаются, и, кроме того, каждый элемент множества В является элементом множества А. В этом случае говорят, что множество В включается в множество А или что множество В является подмножеством множества А и пишут В Ì А.

Определение. Множество В является подмножеством множества А, если каждый элемент множества В является также элементом множества А. Пустое множество считают подмножеством любого множества. Любое множество является подмножеством самого себя.

Из определения следует, что если В Ì А, то множество В может быть пустым, и тогда Æ Ì А, и, кроме того, множество В может совпадать с А, и тогда А Ì А. Поэтому среди всех подмножеств заданного множества А должно быть обязательно пустое множество и само множество А, их называют несобственными.

Образуем, например, все подмножества множества А= {2,3,4}. Среди них будут одноэлементные подмножества: {2}, {3}, {4}, двухэлементные: {2, 3}, {2, 4}, {3, 4}, а также само множество А и пустое множество Æ. Таким образом, данное трехэлементное множество А имеет 8 подмножеств.

Доказано, что если множество А содержит п элементов, то у него 2ⁿ различных подмножеств.

Рассмотрим теперь множества А = {а, b, с, d, е} и В ={с, а, d, b, е). Они пересекаются, и каждый элемент множества A является элементом множества В, т.е. А Ì В, и наоборот, каждый элемент множества В является элементом множества А, т.е. В Ì А. В этом случае говорят, что множества А и В равны и пишут А=В.

Определение. Множества А и В называются равными, если А Ì В и В Ì А.

Из определения следует, что равные множества состоят из одних и тех же элементов и что порядок записи элементов множества не существен.

Отношения между множествами наглядно представляют при помощи особых чертежей, называемых кругами Эйлера. Для этого множества представляют в виде кругов, овалов или любых других геометрических фигур. В том случае, если множества А и В имеют общие элементы, но ни одно из них не является подмножеством другого, их изображают так, как показано на рис. 4,а. Если множество В является подмножеством А, то круг, изображающий множество В, целиком находится в круге, изображающем множество А (рис. 4, б). Если А Ì В, то множества А и В изображают так, как на рисунке 4, в. Равные множества представляют в виде одного круга (рис. 4, г).

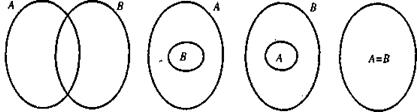
а) б) в) г)

Рис.4

Если множества А и В не пересекаются, то их изображают в виде двух фигур, не имеющих общих точек (рис. 5).

Понятие подмножества является обобщением понятия части и целого, которые осваивают младшие школьники, выполняя разные задания. Например: «Назови среди данных чисел четные», «Среди данных четырехугольников найди прямоугольники».

Упражнения

1. Даны два множества: X = {2,4,6} и Y = {0,2,4,6,8}. Верно ли что:

а) множества X и Y пересекаются;

б) множество X является подмножеством множества Y;

в) множество Р = {4, 0, 6, 8, 2} равно множеству Y?

2. Известно, что элемент а содержится в множестве А и в множестве В. Следует ли из этого, что:

а) А Ì В; б ) В Ì А; в) А = В?

3. Из множества К = {216, 546, 153, 171, 234} выпишите числа, которые:

а) делятся на 3; б) делятся на 9;

в) не делятся на 4; г) не делятся на 5.

Есть ли среди полученных подмножеств такое, которое равно множеству К?

4. Изобразите при помощи кругов Эйлера отношения между множествами С и А если:

а) С-множество двузначных чисел,

D = {3,43, 34, 56, 103};

б) С - множество двузначных чисел,

D- множество четных натуральных чисел;

в) С - множество двузначных чисел,

D - множество трехзначных чисел;

г) С - множество двузначных чисел,

D - множество натуральных чисел, не меньших 10.

5. Отношения между множествами всех выпуклых четырехугольников, параллелограммов, пря­моугольников, ромбов и квадратов изображены на рисунке 6. Покажите каждое из множеств.

6. Дано множество Р = {3, 5, 7, 9}. Образуйте всевозможные его подмножества. Сколько их должно быть?

7. Какое из данных множеств является подмножеством другого:

а) А - множество натуральных чисел, кратных 2,

В - множество натуральных чисел, кратных 6,

С- множество натуральных чисел, кратных 3.

б) А- множество треугольников,

В - множество прямоугольных треугольников,

С- множество остроугольных треугольников.

8. О каких теоретико-множественных понятиях идет речь в следующих заданиях, выполняемых учащимися начальных классов:

а) Запиши по порядку числа от 10 до 19. Подчеркни и прочитай четные числа.

б) Из ряда чисел от 1 до 20 выпиши по порядку числа, которые делятся на 5.

в) Запиши три числа, которые при делении на 7 дают в остатке 4.

Не нашли, что искали? Воспользуйтесь поиском: