Понятие множества и элемента множества

Вматематике часто рассматриваются те или иные группы объектов как единое целое: натуральные числа, треугольники, квадраты и т.д. Все эти различные совокупности называют множествами.

Понятие множества является одним из основных понятий математики и поэтому не определяется через другие. Его можно пояснить на примерах. Так, можно говорить о множестве гласных букв русского алфавита, о множестве натуральных чисел, о множестве треугольников.

Математический смысл слова «множество» отличается от того, как оно используется в обыденной речи, где его связывают с большим числом предметов. В математике этого не требуется. Здесь можно рассматривать множество, состоящее из одного объекта, и множество, не содержащее ни одного объекта.

Множества принято обозначать прописными буквами латинского алфавита: А, В, С,.... Z.

Множество, не содержащее ни одного объекта, называется пустым и обозначается символом Æ.

Объекты, из которых образовано множество, называются элементами.

Элементы множества принято обозначать строчными буквами латинского алфавита: а, b, с,..., z.

В математике нередко приходится выяснять, принадлежит какой-либо объект рассматриваемому множеству или не принадлежит. Например, мы говорим, что 5 - число натуральное, а 0,75 не является натуральным числом. Другими словами, мы утверждаем, что число 5 принадлежит множеству натуральных чисел, а число 0,75 ему не принадлежит. Чтобы записать эти утверждения, вводятся символы Î и Ï. Предложение «Объект а принадлежит множеству А» можно записать, используя символы: а Î А. Предложение «Объект а не принадлежит множеству А» можно записать так: а Ï А.

Например, если А - множество однозначных чисел, то утверждение «Число 3 - однозначное» можно записать в таком виде: 3 Î А. Запись 12Ï А означает, что «Число 12 не является однозначным», или «Число 12 не принадлежит множеству А», или «Множество А не содержит числа 12».

Заметим, что в геометрии, которая возникла значительно раньше теории множеств, если точка является элементом какого-либо множества, то ее обозначают заглавной буквой. Например, если X - множество точек отрезка АВ, то предложение «Точка Р лежит на отрезке АВ» можно записать: Р Î X или Р Î АВ.

Множества бывают конечные и бесконечные. Эти понятия мы принимаем без определения. Поясним их на примерах. Так, конечными являются множество дней недели, множество месяцев в году, а беско­нечными - множество точек на прямой, множество натуральных чисел..

Для ряда числовых множеств в математике приняты стандартные обозначения:

N - множество натуральных чисел;

Z - множество целых чисел;

Q - множество рациональных чисел;

R - множество действительных чисел.

Упражнения

1. Назовите три элемента множества:

а) учебных предметов, изучаемых в начальной школе;

б) четных натуральных чисел;

в) четырехугольников.

2. Запишите, используя символы:

а) Число 14 - натуральное;

б) Число -7 не является натуральным;

в) Число 0 - рациональное;

г) √7 - число действительное.

3. Прочитайте следующие высказывания и укажите среди них вер­ные:

а) 100 Î N; г) 5,36 Î Q; ж) -7,3 Î R;

б)-8 Î Z; д)102Ï R; з) 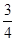Î N;

в)-12 Ï N; е) √2 Î Q; и)0Î N.

4. Р - множество натуральных чисел, больших 7 и меньше 14. Выясните, какие из чисел 13, 10, 5, 7, 14 ему принадлежат, а какие не принадлежат. Ответ запишите, используя знаки Î и Ï..

4. Даны числа: 0; 7; -3,8; -17; 325; √5. Установите, какие из них:

а) натуральные; в) рациональные;

б) целые; г) действительные.

6. М - множество точек окружности, изображенной на рисунке 1. Прочитайте следующие предложения и укажите среди них верные:

а) А Î М; б) О Î М;

в) В Î М; г) С Ï М.

7. Как изменить условие задачи 6, чтобы все утверждения а) - г) были верными?

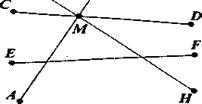
8. Запишите с помощью знаков Î и Ï, какие из отрезков АВ, СД ЕЕ и РН проходят через точку М, а какие через нее не проходят (рис. 2).

9. А - множество решений уравнения х² + 1 = 0. Верно ли, что А - пустое множество? Приведите пример уравнения, множество решений которого состоит из:

а) одного элемента;

б) двух элементов;

в) трех элементов.

10. Запишите множество букв в слове «математика» и множество цифр в записи числа 5125353.

Не нашли, что искали? Воспользуйтесь поиском: