
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Коллинеар векторлар. 3 страница














Жүйе матрицасы мен кеңейтілген матрицаның екінші ретті нолге тең емес минорлары бар екенін көру қиын емес және  . Кронеккер-Капелли теоремасы бойынша жүйе үйлесімді. Жүйе рангісі r=2, ал белгісіздер саны n=4, r<n болғандықтан жүйе анықталмаған, яғни шексіз көп шешімі бар.
. Кронеккер-Капелли теоремасы бойынша жүйе үйлесімді. Жүйе рангісі r=2, ал белгісіздер саны n=4, r<n болғандықтан жүйе анықталмаған, яғни шексіз көп шешімі бар.
21. Қандай жүйе үйлесімсіз деп аталады? Негізгі ұғымдар мен анықтамалар. n белгісізді m теңдеуден тұратын жүйе деп мынадай жүйені айтады:  (1)мұндағы
(1)мұндағы  (i=1,2,…,m, j=1,2,…,n) - теңдеу коэффициенттері деп, ал
(i=1,2,…,m, j=1,2,…,n) - теңдеу коэффициенттері деп, ал  (i=1,2,…,m) - бос мүшелері деп аталады. (1) теңдеудің қысқаша жазылуы мынадай:
(i=1,2,…,m) - бос мүшелері деп аталады. (1) теңдеудің қысқаша жазылуы мынадай:  (i=1,2,…,m)
(i=1,2,…,m)
жүйенің бос мүшелерінің бәрі нолге тең болса,  (i=1,2,…,m) жүйе біртекті жүйе деп аталады. Жүйенің әрбір теңдеуін тепе-теңдікке айналдыратын
(i=1,2,…,m) жүйе біртекті жүйе деп аталады. Жүйенің әрбір теңдеуін тепе-теңдікке айналдыратын 


сандар тізбегі теңдеулер жүйесінің шешімі деп аталады. Осы шартты қанағаттандыратын барлық  шешімдер шешімдер жиынын құрады. Жүйенің шешімдер жиынын табу процесін жүйені шешу дейді.
шешімдер шешімдер жиынын құрады. Жүйенің шешімдер жиынын табу процесін жүйені шешу дейді.
(1) жүйенің ең болмағанда бір шешімі болса жүйе үйлесімді, ал шешімі болмаса үйлесімсіз деп аталады. Үйлесімді жүйенің бір ғана шешімі болса, жүйе анықталған, ал шешімі бірден көп болса анықталмаған деп аталады. Енді (1) жүйеге мынадай белгілеулер енгізейік:
 ,
,  ,
, 
А - жүйе коэффициенттерінен құрылған матрица немесе жүйе матрицасы, Х - жүйенің бос мүшелерінен құрылған бағана матрица, В - жүйенің бос мүшелерінен құрылған бағана матрица. Осы белгілеулерді қолданып (1) жүйені былайша жазуға болады: АХ=В (3). (3) теңдеу (1) жүйенің матрицалық жазылуы болып табылады. Егер жүйе матрицасына бос мүшелер матрицасын жалғап жазсақ,

 , жүйенің кеңейтілген матрицасын аламыз.
, жүйенің кеңейтілген матрицасын аламыз.
Кронеккер-Капелли теоремасы. Егер сызықты теңдеулер жүйесінің негізгі матрицасы мен кеңейтілген матрицасының ранглері тең болса, онда жүйе үйлесімді болады.
Теорема бойынша жүйе үйлесімді болуы үшін  болуы керек. Бұл кезде r жүйе рангісі деп аталады.
болуы керек. Бұл кезде r жүйе рангісі деп аталады.
Үйлесімді жүйенің рангісі жүйедегі белгісіздер санына тең болса (r=n), онда жүйе анықталған болады, ал егер жүйенің рангісі жүйедегі белгісіздер санынан кем болса (r<n), онда жүйе анықталмаған болады. Мысалы, мынадай жүйе қарастырайық:
 Жүйенің кеңейтілген матрицасын жазып, элементар түрлендірулер жасайық:
Жүйенің кеңейтілген матрицасын жазып, элементар түрлендірулер жасайық:














Жүйе матрицасы мен кеңейтілген матрицаның екінші ретті нолге тең емес минорлары бар екенін көру қиын емес және  . Кронеккер-Капелли теоремасы бойынша жүйе үйлесімді. Жүйе рангісі r=2, ал белгісіздер саны n=4, r<n болғандықтан жүйе анықталмаған, яғни шексіз көп шешімі бар.
. Кронеккер-Капелли теоремасы бойынша жүйе үйлесімді. Жүйе рангісі r=2, ал белгісіздер саны n=4, r<n болғандықтан жүйе анықталмаған, яғни шексіз көп шешімі бар.
22.Сызықтық теңдеулер жүйесін шешу тәсілдері: Крамер әдісі: Бұл әдіс жүйедегі теңдеулер саны мен белгісіздер саны тең болғанда, яғни m=n, қолдануға болады. Демек, жүйе түрі мынадай болады:
 (4)
(4)
Жүйедегі теңдеулер саны мен белгісіздер саны тең, онда жүйе матрицасы квадрат матрица болады. Сол квадрат матрицаның анықтауышын  деп белгілейік:
деп белгілейік:

Крамер ережесі.  -жүйе анықтауышы, ал
-жүйе анықтауышы, ал  -
-  анықтауыштың j-тік жолын бос мүшелермен алмастырғаннан пайда болған анықтауыш болсын. Сонда, егер
анықтауыштың j-тік жолын бос мүшелермен алмастырғаннан пайда болған анықтауыш болсын. Сонда, егер  болса жүйенің жалғыз шешімі бар болады және мынадай формуламен табылады:
болса жүйенің жалғыз шешімі бар болады және мынадай формуламен табылады:
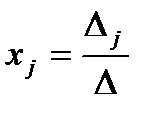 (i=1,2,…,n) формуланы Крамер формуласы деп атайды.
(i=1,2,…,n) формуланы Крамер формуласы деп атайды.
Осы ережені қолданып мынадай жүйені шешейік

Шешуі. Алдымен  анықтауышты есептейміз,
анықтауышты есептейміз,
 .т
.т  (j=1,2,3) анықтауыштарды есептейік
(j=1,2,3) анықтауыштарды есептейік
 ,
,  ,
, 
Енді Крамер формуласын қолданып белгісіздерді табамыз:
 ,
,  ,
,  .
.
Сонымен, берілген жүйенің жалғыз (-1; 2; 3) шешімі табылды, жүйе анықталған екен.
Матрицалық әдіс: Бұл әдіс те жүйедегі теңдеулер саны мен белгісіздер саны тең болғанда, яғни m=n, қолдануға болады. Жүйенің матрицалық жазылуын
қарастырайық: АХ
=В, мұндағы, 
 ,
,  .
.
Айталық А ерекше емес матрица болсын, яғни матрица анықтауышы нолге тең емес, олай болса әр уақытта  кері матрицасы бар болады. Теңдеуді сол жағынан кері матрицаға көбейтейік,
кері матрицасы бар болады. Теңдеуді сол жағынан кері матрицаға көбейтейік,  АХ=
АХ=  В
В  А=E болатындықтан, ЕХ=
А=E болатындықтан, ЕХ=  В, кез келген матрицаның бірлік матрицаға көбейтіндісі сол матрицаның өзіне тең болатындықтан, ЕХ=Х:Х=
В, кез келген матрицаның бірлік матрицаға көбейтіндісі сол матрицаның өзіне тең болатындықтан, ЕХ=Х:Х=  В. Сонымен, кері матрицалық әдіс бойынша жүйенің шешімін табу үшін бос мүшелерден құралған матрицаны жүйе матрицасының кері матрицасына көбейту керек екен. Жоғарыда карастырылған
В. Сонымен, кері матрицалық әдіс бойынша жүйенің шешімін табу үшін бос мүшелерден құралған матрицаны жүйе матрицасының кері матрицасына көбейту керек екен. Жоғарыда карастырылған 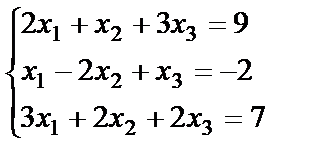 жүйені осы әдіс бойынша шешіп көрейік.
жүйені осы әдіс бойынша шешіп көрейік.
Шешуі.  болғандықтан, жүйе матрицасы ерекше емес. Осы матрицаның кері матрицасын табамыз:
болғандықтан, жүйе матрицасы ерекше емес. Осы матрицаның кері матрицасын табамыз:
 .
.
Енді Х=  В теңдікті қолданып белгісіздерді табамыз:
В теңдікті қолданып белгісіздерді табамыз:




 .
.
Сонымен,  ,
,  ,
,  шешімдері табылды.
шешімдері табылды.
Гаус әдісімен шешу: n белгісізді m теңдеуден тұратын жүйе қарастырайық,
 .
.
Гаусс әдісі - жүйедегі айнымалыларды түрлендірулер көмегімен біртіндеп жойып, жүйені сатылы түрге келтіріп, айнымалыларды біртіндеп табатын әдіс. Гаусс түрлендірулері мынадай:
1. Кез келген екі теңдеудің орындарын ауыстырып жазу;
2. Кез келген теңдеудің екі жағын нолден өзге санға көбейту;
3. Қандай да бір теңдеуді нолден өзге санға көбейтіп, басқа теңдеуге сәйкесінше қосу;
4. 0=0 түріндегі теңдеуді сызып тастау.
Гаусс түрлендірулерін жүйенің өзіне қолданғаннан гөрі оның кеңейтілген матрицасына қолданған ұтымды болады. Олай болса жүйенің кеңейтілген матрицасын қарастырайық,
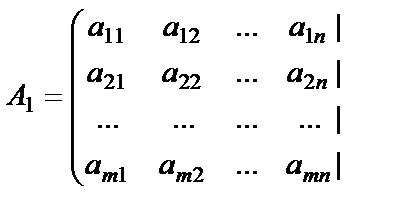
 . Осы матрицаны түрлендірулер нәтижесінде мынадай түргекелтіреміз:
. Осы матрицаны түрлендірулер нәтижесінде мынадай түргекелтіреміз: 


Матрицаның элементтері  арқылы белгіленіп тұрғанымен, шын мәнінде олар түрлендірулер нәтижесінде өзгерген. Бұл белгілеулер жазуды ықшамдау үшін ғана пайдаланылып отыр.
арқылы белгіленіп тұрғанымен, шын мәнінде олар түрлендірулер нәтижесінде өзгерген. Бұл белгілеулер жазуды ықшамдау үшін ғана пайдаланылып отыр.
Соңғы матрицаға сәйкес келетін теңдеулер жүйесі мынадай:
 (6)
(6)
Соңғы  ,...,
,...,  теңдеулеріндегі
теңдеулеріндегі  ,...,
,...,  сандарының ең болмағанда біреуі нөлден өзгеше болса, онда берілген теңдеулер жүйесі үйлесімсіз, ал бәрі нолге тең болса жүйе үйлесімді болады.
сандарының ең болмағанда біреуі нөлден өзгеше болса, онда берілген теңдеулер жүйесі үйлесімсіз, ал бәрі нолге тең болса жүйе үйлесімді болады.
Жүйенің рангісі жүйедегі белгісіздер санынан кем болса, онда жүйе анықталмаған болатыны жоғарыда айтылған. Айталық (6) жүйе үйлесімді және r<n болсын. Егер 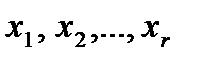 коэффициенттерінен құрылған анықтауыш нолден өзгеше болса, онда
коэффициенттерінен құрылған анықтауыш нолден өзгеше болса, онда 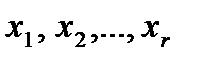 айнымалыларды базистік (негізгі) айнымалылар деп, ал басқа n-r айнымалыларды еркін (негізгі емес) айнымалылар деп атайды. Еркін айнымалылары нолге тең болған кездегі шешім базистік шешім деп аталады. Базистік шешімдер саны
айнымалыларды базистік (негізгі) айнымалылар деп, ал басқа n-r айнымалыларды еркін (негізгі емес) айнымалылар деп атайды. Еркін айнымалылары нолге тең болған кездегі шешім базистік шешім деп аталады. Базистік шешімдер саны  -ден артпайды.
-ден артпайды.
1-мысал.  Шешуі. Жүйенің кеңейтілген матрицасын жазып, элементар түрлендірулер жасайық:
Шешуі. Жүйенің кеңейтілген матрицасын жазып, элементар түрлендірулер жасайық:















 .
.
Соңғы матрицаға сәйкес келетін жүйе жазайық: 
Сонымен жүйенің шешімі табылды: 
23. Вектордың анықтамасы. Басы А, соңы В нүктесі болатын бағытталған кесінді вектор деп аталады. Оқулықтарда векторларды  немесе
немесе 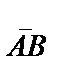 , кейде тек қалың әріптермен АВ белгілеу түрлері кездеседі. Сол сияқты векторларды бір әріппен де белгілей береді (
, кейде тек қалың әріптермен АВ белгілеу түрлері кездеседі. Сол сияқты векторларды бір әріппен де белгілей береді ( =
=  ,
,  , а).
, а).  векторының ұзындығы деп АВ кесіндісінің ұзындығын айтады және
векторының ұзындығы деп АВ кесіндісінің ұзындығын айтады және  деп белгілейді. Басы мен соңы беттесетін вектор нолдік вектор деп аталады,
деп белгілейді. Басы мен соңы беттесетін вектор нолдік вектор деп аталады,  =
=  және ұзындығы нолге тең.Бір түзудің не өзара параллель түзулер бойында орналасқан векторлар коллениар векторлар деп аталады.
және ұзындығы нолге тең.Бір түзудің не өзара параллель түзулер бойында орналасқан векторлар коллениар векторлар деп аталады.  және
және  векторларының қосындысы «үшбұрыш» не «параллелограмм» ережесімен анықталады:
векторларының қосындысы «үшбұрыш» не «параллелограмм» ережесімен анықталады:

|
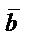
|

|

|

|

|
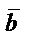
|

|
 және
және  векторларының
векторларының  -
-  айырымы деп
айырымы деп  -ға қосқанда
-ға қосқанда 
векторы алынатын 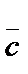 =
=  -
-  векторын айтады.
векторын айтады.
 векторының
векторының 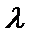 санға көбейтіндісі деп ұзындығы
санға көбейтіндісі деп ұзындығы  болатын, бағыты
болатын, бағыты 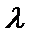 >0 болғанда
>0 болғанда  векторымен бағыттас,
векторымен бағыттас, 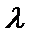 <0 болғанда
<0 болғанда  векторымен қарама-қарсы бағытта болатын
векторымен қарама-қарсы бағытта болатын  векторын айтады. Суретте,
векторын айтады. Суретте, 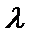 = 2,
= 2,  =2
=2  ;
; 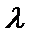 = -1,
= -1,  =-
=-  .
.
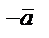
|

|

|
Вектордың ұзындығы оның координаталарының квадраттарының қосындысынан алынған квадрат түбірге тең: 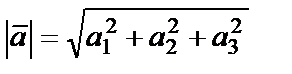 .
.  және
және  векторлары координаталарымен берілген болса олардың қосындысы мынадай түрде анықталады:
векторлары координаталарымен берілген болса олардың қосындысы мынадай түрде анықталады: 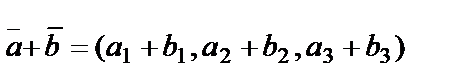 .Ал
.Ал  векторын
векторын 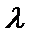 санға көбейту мынадай түрде анықталады:
санға көбейту мынадай түрде анықталады: 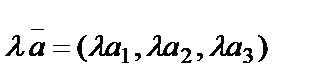 .
.  және
және  векторларының скаляр көбейтіндісі мынадай:
векторларының скаляр көбейтіндісі мынадай:
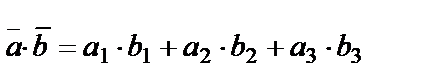
Вектордың ұзындығының формуласы:  АВ
АВ  =
=  2+
2+  2+
2+  2
2
Вектор деп бағытталған кесіндіні атаймыз. Яғни AB вектордың A басы мен B ұшы бар болады:
В
А+В
А
Мысалы D(5; 4)
3CD
1 С(1;1)
1 2 3 4 5
Вектордың басы мен ұшының арақашықтығы оның (вектордың) ұзындығы немесе абсолюттік шамасы деп аталады.
Мысалы жоғарыдағы CD векторының |CD| ұзындығы:
CD|=  2+(4-1)2
2+(4-1)2
|CD|=  2+32
2+32
|CD|= 
|CD|= 
|CD|=5
Егер вектордың басы мен ұшы бір нүктеде орналасса онда бұндай векторды нөлдік вектор деп атайды. Өйткені бұндай вектордың ұзындығы нөлге тең.
Вектордың координаттары деп оның (вектордың) ұшының және басының сәйкесінше координаттарының айырмасын атаймыз.
Яғни AB векторының басы A(x1, y1) нүктесі ал ұшы B(x2, y2) нүктесі болса онда AB векторының координаттары (x2-x1, y2 –y1) болады.
Мысалы жоғарыдағы CD векторының координаттары (5-1; 4-1)=(4; 3).
Геометрияда сәйкесінше координаттары бірдей векторларды бірдей векторлар деп санайды.
Соңдықтан векторларды a, b, c,… деп бір ғана әріппен белгілейміз. a векторының координаттарын (aХ, aУ) деп белгілейміз. Ал a векторының өзін кейде {aХ, aУ} деп те белгілейміз
25. Вектордың орты. Өзінің сандық мәнімен қоса кеңістіктегі бағытымен де сипатталатын шамалар векторлық шамалар немесе векторлар деп аталады.
Сонымен, орын ауыстыру векторлық шама болып табылады. Векторларды бағытталған кесінді түрінде кескіндейді және бір әріппен немесе вектордың басы мен ұшын көрсететін екі әріппен белгілеп, төбесіне нұскама (стрелка) қояды. Мысалы жылдамдық векторын ʋ немесе АВ, күш векторын F немесе CD түрінде кескіндеуге болады.
Кеңістікте белгілі бір бағыты болмайтын, тек сандық мәнімен ғана сипатталатын шаталар скалярлық шамалар немесе скалярлар деп аталады. Мысалы, уақыт, заттың тығыздығы, дененің көлемі, температура, арақашықтығын (орын ауыстыру емес), сынып бөлмесінің ұзындығы, ені және биіктігі, т.с.с. скалярлық шамаларға жатады.
Кез келген вектордың сандық мәні оның модулі деп аталады.Модуль — скалярлық шама.
Не нашли, что искали? Воспользуйтесь поиском: