
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Коллинеар векторлар. 8 страница.

|

|

|

|

|

|

|
| 4-сурет |

| 4-сурет |
 осыдан
осыдан  .
.
Енді алынған өрнектегі х пен у орындарын алмастырамыз:  .Сонда берілген
.Сонда берілген  ф-ға кері функция
ф-ға кері функция  болады.
болады.
Берілген функцияның анықталу облысы оған кері функцияның мәндер жиыны болады да, мәндер жиыны кері функцияның анықталу облысы болады.Аралықта монотонды өсетін немесе монотонды кемитін функциялардың ғана кері функциялары табылады.
6. Күрделі функция. y=f(g(x)) түрінде берілген функцияны күрделі функция дейді. Кейде күрделі функцияны мынадай түрде де береді: y=f(u) мұндағы u=g(x). Бұл жағдайда u - аралық айнымалы, ал х -тәуелсіз аргумент болады.
Мысалы,  ф-сы күрделі функция. Оны
ф-сы күрделі функция. Оны  , мұндағы
, мұндағы  түрінде жазуға болады.
түрінде жазуға болады.
7. Айқын емес түрде берілген функция. Егер функция F(x,y)=0, яғни y айнымалыға қатысты шешілмеген түрінде, берілсе функция айқын емес түрде берілген дейміз. Жоғарыда қарастырылған  функцияны айқын емес түрде былай жазамыз:
функцияны айқын емес түрде былай жазамыз:  .
.
59. Кері функция. Кері функция. y=f(x) функциясының кері функциясын табу үшін алдымен х аргументті у айнымалы арқылы өрнектейміз, х=g(у), одан кейін, тәуелсіз аргумент х деп ал ал тәуелді айнымалы у деп белгілеу қалыптасқандықтан, алынған өрнектегі х пен у орындарын алмастырамыз, у=g(х). Пайда болған g(х) функция берілген f(x) функцияға кері функция болады.
Өзара кері функциялардың графигі y=x (бірінші және үшінші декарттық бұрыштардың биссектрисасы) түзуіне қарағанда симметриялы болады.

|

|

|

|

|

|

|
| 4-сурет |

| 4-сурет |
 осыдан
осыдан  .
.
Енді алынған өрнектегі х пен у орындарын алмастырамыз:  .Сонда берілген
.Сонда берілген  ф-ға кері функция
ф-ға кері функция  болады.
болады.
Берілген функцияның анықталу облысы оған кері функцияның мәндер жиыны болады да, мәндер жиыны кері функцияның анықталу облысы болады.Аралықта монотонды өсетін немесе монотонды кемитін функциялардың ғана кері функциялары табылады.
60. Айқындалмаған функция. Айқындалмаған функция және оның туындысы.
Айталық  теңдеуі берілсін. Мұнда
теңдеуі берілсін. Мұнда  х-тен тәуелді функция. Бұл жағдайда
х-тен тәуелді функция. Бұл жағдайда  айқындалмай берілген функция дейді.(8.3) формуланы пайдаланып
айқындалмай берілген функция дейді.(8.3) формуланы пайдаланып  (8.9) теңдеуді шығарамыз. Осыдан
(8.9) теңдеуді шығарамыз. Осыдан 
(8.10) айқындап берілмеген функцияның туындысы.
Мысалы:  теңдеуі берілсін. Мұнда
теңдеуі берілсін. Мұнда 
 онда
онда 
61. Функцияның нүктедегі шегі. Анықтама.
Егер алдын ала берілген, мейілінше аз 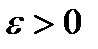 санына
санына 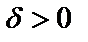 саны табылып,
саны табылып, 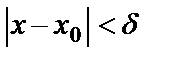 шартын қанағаттандыратын барлық х үшін
шартын қанағаттандыратын барлық х үшін  теңсіздігі орындалса, онда А саны f(x) функциясының х аргумент х0-ге ұмтылғандағы шегі деп аталады да, былай жазылады:
теңсіздігі орындалса, онда А саны f(x) функциясының х аргумент х0-ге ұмтылғандағы шегі деп аталады да, былай жазылады: 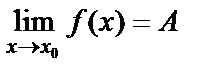 . Анықтамадағы
. Анықтамадағы  теңсіздікті ашсақ, мынадай қос теңсіздік аламыз:
теңсіздікті ашсақ, мынадай қос теңсіздік аламыз: 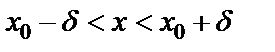 .
. 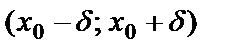 интервалды
интервалды  нүктесінің
нүктесінің  -маңайы дейді. Сол сияқты
-маңайы дейді. Сол сияқты 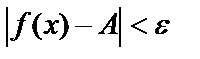 теңсіздікті ашсақ:
теңсіздікті ашсақ: 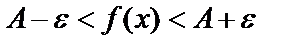 .
. 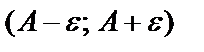 интервалды А нүктесінің
интервалды А нүктесінің 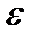 -маңайы дейді.Енді анықтаманы сурет бойынша айтсақ: Алдын ала берілген,
-маңайы дейді.Енді анықтаманы сурет бойынша айтсақ: Алдын ала берілген,  санына
санына 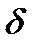 саны табылып, аргумент мәндері
саны табылып, аргумент мәндері  нүктесінің
нүктесінің  -маңайына тиісті болғанда функцияның сәйкес мәндері А нүктесінің
-маңайына тиісті болғанда функцияның сәйкес мәндері А нүктесінің 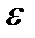 -маңайында жатса, А саны f(x) функциясының х аргумент х0 -ге ұмтылғандағы шегі деп аталады. Мысал. Өндіріс орны шығаратын заттың бір данасының бағасы y пен оған деген сұраныс x (мың дана) арасындағы байланыс мынадай қатынаспен анықталған:
-маңайында жатса, А саны f(x) функциясының х аргумент х0 -ге ұмтылғандағы шегі деп аталады. Мысал. Өндіріс орны шығаратын заттың бір данасының бағасы y пен оған деген сұраныс x (мың дана) арасындағы байланыс мынадай қатынаспен анықталған:  .
.
| у 210 200 190 0 11,4 12 12,6 х |
Шешуі. (190; 210) интервалының ортасы А=200 теңге, олай болса  = 10. Шек анықтамасындағы
= 10. Шек анықтамасындағы 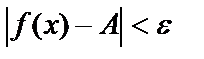 теңсіздігін қолданайық:
теңсіздігін қолданайық: 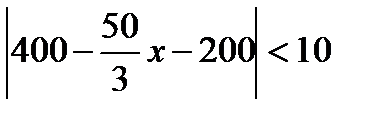 . Осы теңсіздікті түрлендіріп ықшамдасақ мынадай теңсіздік аламыз:
. Осы теңсіздікті түрлендіріп ықшамдасақ мынадай теңсіздік аламыз: 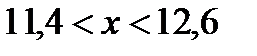 .
.
Соңғы теңсіздікті мынадай 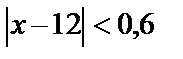 түрге келтіріп жазсақ, есеп сұрағына жауап беруге болады: Заттың бір данасының бағасының 200 теңгеден ауытқуы 10 теңгеден артпауы үшін, өндіріс орны өнім көлемінің өзгеруін 0,6 мың данадан асырмауы керек екен.
түрге келтіріп жазсақ, есеп сұрағына жауап беруге болады: Заттың бір данасының бағасының 200 теңгеден ауытқуы 10 теңгеден артпауы үшін, өндіріс орны өнім көлемінің өзгеруін 0,6 мың данадан асырмауы керек екен.
Функция шегінің қасиеттері.
Айталық 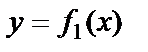 және
және  функцияларының
функцияларының 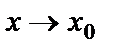 жағдайда
жағдайда  және
және 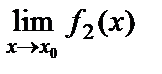 шектері бар болсын.
шектері бар болсын.
1. Екі функцияның алгебралық қосындысының шегі шектердің алгебралық қосындысына тең болады, яғни
2. 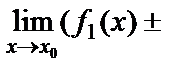
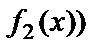 =
= 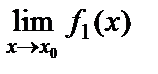
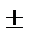
 .
.
3. Екі функцияның көбейтіндісінің шегі шектердің көбейтіндісіне тең болады, яғни
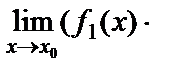
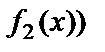 =
= 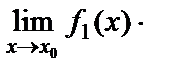
 .
.
Салдар. 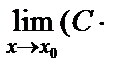
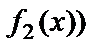 = С
= С  , мұндағы С - const.
, мұндағы С - const.
4. Екі функцияның қатынасының шегі шектердің қатынасына тең болады (әрине, егер бөлімдегі функция нолден өзгеше болса), яғни 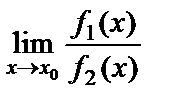 =
= 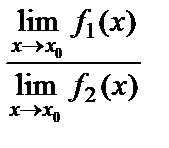 .
.
5. Мысал. 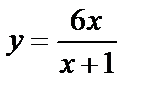 функциясының
функциясының  жағдайдағы шегін табу керек.
жағдайдағы шегін табу керек.
6. Шешуі. Қысқаша айтсақ 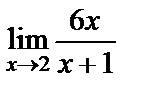 шек есептеу керек. Функция шегінің қасиеттерін қолданып есептейік:
шек есептеу керек. Функция шегінің қасиеттерін қолданып есептейік: 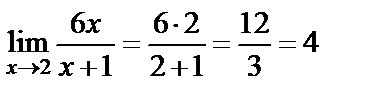 .
. 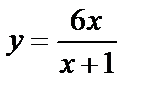 функциясының
функциясының  жағдайдағы шегі 4 болады екен.
жағдайдағы шегі 4 болады екен.
62. Функцияның ақырсыздықтағы шегі. АҚЫРСЫЗ АЗ ЖӘНЕ АҚЫРСЫЗ ҮЛКЕН ФУНКЦИЯЛАР
Анықтама.  функциясының
функциясының  жағдайда шегі ноль болса, яғни
жағдайда шегі ноль болса, яғни 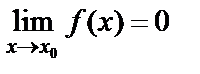 , онда
, онда  функциясы
функциясы  жағдайда ақырсыз аз функция деп аталады.
жағдайда ақырсыз аз функция деп аталады.
Осы анықтаманы “  ” тілінде былай да айтуға болады: Кез келген
” тілінде былай да айтуға болады: Кез келген  үшін
үшін  саны табылып,
саны табылып,  теңсіздігін қанағаттандыратын барлық х-тер үшін
теңсіздігін қанағаттандыратын барлық х-тер үшін  теңсіздігі орындалса,
теңсіздігі орындалса,  функциясы
функциясы  жағдайда ақырсыз аз функция деп аталады.
жағдайда ақырсыз аз функция деп аталады.
Ақырсыз аз функция қасиеттері.
1.Егер  функциясының
функциясының  жағдайда А шегі бар болса, онда
жағдайда А шегі бар болса, онда  функциясын осы А саны мен
функциясын осы А саны мен  жағдайда ақырсыз аз болатын
жағдайда ақырсыз аз болатын  функцияқосындысы түрінде жазуға болады,яғни
функцияқосындысы түрінде жазуға болады,яғни 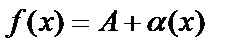 .
.
1. Ақырсыз аз функцияның шенелген функцияға (сонмен қатар, тұрақтыға, басқа ақырсыз азға) көбейтіндісі ақырсыз аз функция болады.
2. Ақырсыз аз функцияның шегі нолден өзге функцияға қатынасы ақырсыз аз функция болады.
Анықтама.  функциясының
функциясының  жағдайда шегі шексіздік болса, яғни
жағдайда шегі шексіздік болса, яғни  , онда
, онда  функциясы
функциясы  жағдайда ақырсыз үлкен функция деп аталады.
жағдайда ақырсыз үлкен функция деп аталады.
Ақырсыз аз функция мен ақырсыз үлкен функция арасында мынадай байланыс бар: Егер  функциясы
функциясы  жағдайда ақырсыз аз болса,
жағдайда ақырсыз аз болса,  функциясы
функциясы  жағдайда ақырсыз үлкен болады. Мысалы,
жағдайда ақырсыз үлкен болады. Мысалы,  функциясы
функциясы  жағдайда ақырсыз аз функция болады. Шынында да,
жағдайда ақырсыз аз функция болады. Шынында да,  шегін есептейік.
шегін есептейік.  .
.
Ал  функциясы
функциясы  жағдайда ақырсыз үлкен функция болады, яғни оның шегі шексіздік. Шынында да, шегін есептейік.
жағдайда ақырсыз үлкен функция болады, яғни оның шегі шексіздік. Шынында да, шегін есептейік. 
 .
.
Мұндағы 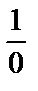 қатынасты шектер тілінде “ақырсыз азға кері шама ақырсыз үлкен” дейді де, шексіздікке теңестіреді.
қатынасты шектер тілінде “ақырсыз азға кері шама ақырсыз үлкен” дейді де, шексіздікке теңестіреді.
Ақырсыз аз функциялар нолге әртүрлі жылдамдықпен жақындайды. Көптеген жағдайда ақырсыз аздардың нолге ұмтылу жылдамдығын анықтау үшін оларды өзара салыстыру керек болады. Салыстыру үшін олардың қатынасының  жағдайдағы шегін қарастырады.
жағдайдағы шегін қарастырады.
Ақырсыз аздарды салыстыру
Айталық 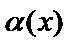 және
және 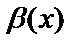
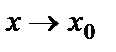 жағдайда ақырсыз аз функциялар және
жағдайда ақырсыз аз функциялар және 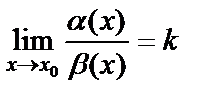 болсын. Онда, егер
болсын. Онда, егер
1) 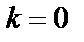 болса
болса 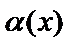
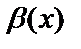 -ға қарағанда жоғары ретті ақырсыз аз деп;
-ға қарағанда жоғары ретті ақырсыз аз деп;
2) 
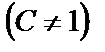 болса
болса  мен
мен  бірдей ретті ақырсыз аз деп;
бірдей ретті ақырсыз аз деп;
3) 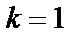 болса
болса 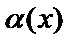 мен
мен  эквивалентті ақырсыз аз деп
эквивалентті ақырсыз аз деп
аталады. 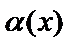 мен
мен 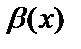 эквивалентті дегенді
эквивалентті дегенді 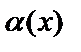 ~
~ 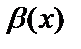 депжазады.
депжазады.
Егер 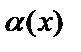 функциясы
функциясы  жағдайда ақырсыз аз болса, онда
жағдайда ақырсыз аз болса, онда
1. 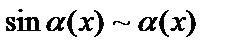 ,
,  ,
,
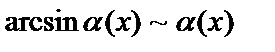 ,
,  ;
;
2.  ,
, 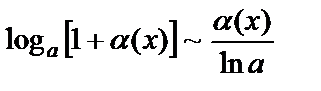 ;
;
3. 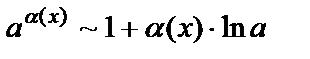 ,
,  ;
;
4. 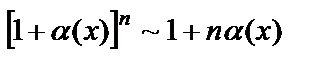 ,
, 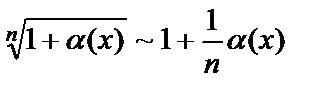 ;
;
5. 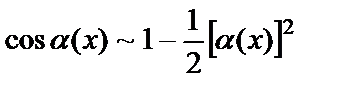 .
.
1.-5. қатынастар эквивалентті функциялар кестесін береді. Бұл кестені шек есептеу кезінде мына теоремаға сүйеніп қолдануға болады.
Теорема. Егер 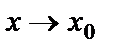 жағдайда
жағдайда 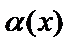 ~
~  және
және 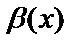 ~
~  болса, онда
болса, онда 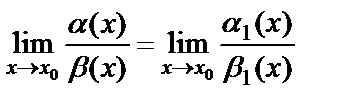 .
.
Мысал. 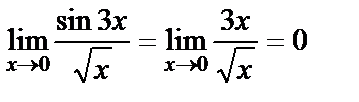 . Мұнда
. Мұнда 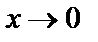 жағдайда
жағдайда 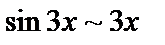 болғандықтан
болғандықтан  орнына
орнына 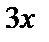 алынды.
алынды.
63. Шексіз үлкен және шексіз аз шамалар. Анықтама.  функциясының
функциясының  жағдайда шегі ноль болса, яғни
жағдайда шегі ноль болса, яғни 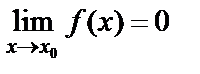 , онда
, онда  функциясы
функциясы  жағдайда ақырсыз аз функция деп аталады.
жағдайда ақырсыз аз функция деп аталады.
Осы анықтаманы “  ” тілінде былай да айтуға болады: Кез келген
” тілінде былай да айтуға болады: Кез келген  үшін
үшін  саны табылып,
саны табылып,  теңсіздігін қанағаттандыратын барлық х-тер үшін
теңсіздігін қанағаттандыратын барлық х-тер үшін  теңсіздігі орындалса,
теңсіздігі орындалса,  функциясы
функциясы  жағдайда ақырсыз аз функция деп аталады.
жағдайда ақырсыз аз функция деп аталады.
Ақырсыз аз функция қасиеттері.
3. Егер  функциясының
функциясының  жағдайда А шегі бар болса, онда
жағдайда А шегі бар болса, онда  функциясын осы А саны мен
функциясын осы А саны мен  жағдайда ақырсыз аз болатын
жағдайда ақырсыз аз болатын  функцияқосындысы түрінде жазуға болады,яғни
функцияқосындысы түрінде жазуға болады,яғни 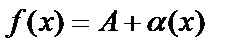 .
.
4. Ақырсыз аз функцияның шенелген функцияға (сонмен қатар, тұрақтыға, басқа ақырсыз азға) көбейтіндісі ақырсыз аз функция болады.
5. Ақырсыз аз функцияның шегі нолден өзге функцияға қатынасы ақырсыз аз функция болады.
Анықтама.  функциясының
функциясының  жағдайда шегі шексіздік болса, яғни
жағдайда шегі шексіздік болса, яғни  , онда
, онда  функциясы
функциясы  жағдайда ақырсыз үлкен функция деп аталады.
жағдайда ақырсыз үлкен функция деп аталады.
Ақырсыз аз функция мен ақырсыз үлкен функция арасында мынадай байланыс бар: Егер  функциясы
функциясы  жағдайда ақырсыз аз болса,
жағдайда ақырсыз аз болса,  функциясы
функциясы  жағдайда ақырсыз үлкен болады. Мысалы,
жағдайда ақырсыз үлкен болады. Мысалы,  функциясы
функциясы  жағдайда ақырсыз аз функция болады. Шынында да,
жағдайда ақырсыз аз функция болады. Шынында да,  шегін есептейік.
шегін есептейік.  .
.
Ал  функциясы
функциясы  жағдайда ақырсыз үлкен функция болады, яғни оның шегі шексіздік. Шынында да, шегін есептейік.
жағдайда ақырсыз үлкен функция болады, яғни оның шегі шексіздік. Шынында да, шегін есептейік. 
 .
.
Не нашли, что искали? Воспользуйтесь поиском: