
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Коллинеар векторлар. 11 страница. 77. Анықталмаған интегралды есептеу
77. Анықталмаған интегралды есептеу тәсілдері. Анықталмағанинтегралқасиеттері.Интеграланықтамасынанмынадайқасиеттершығады.1..2..3. = F(x)+C. 4. Берілгенаралықта f(x) және g(x) функцияларыныңалғашқыфункцияларыбарболса, онда f(x)+g(x) функциясыныңдаалғашқыфункциясыбарболадыжәне5.. 6. Егер = F(x)+C болса, онда = F(ax+b)+C. 7. Егеринтеграластындағыфункцияныңалымыбөлімніңтуындысыболса, ондаинтегралбөлімніңабсолютшамасыныңнатураллогарифмінетең, яғни,мұндағы u=u(x).Анықталмағанинтегралдаркестесі:
 = C = C
| 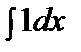 = x + C = x + C
| ||
 = =  + C, x>0, + C, x>0, 
|  =ln| x |+ C, x =ln| x |+ C, x 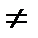 0 0
| ||
 = =  + C, + C, 
|  = =  + C + C
| ||
 = sinx + C = sinx + C
|  =- cosx + C =- cosx + C
| ||
 = tgx + C, = tgx + C, 
|  =- ctgx + C, =- ctgx + C, 
| ||
 = arcsinx + C,
-1<x<1 = arcsinx + C,
-1<x<1
|  = arcsin = arcsin  + C,
-a<x<a + C,
-a<x<a
| ||
 = arctgx + C = arctgx + C
|  = =  artg artg  + C + C
| ||
 = =  ln ln  + C + C
|  ln ln  +C +C
|
78. Анықталған интеграл және оның қасиеттері. Анықтама. y=f(x) функциясының интегралдық қосындысының  жағдайдағы шегі функцияның [a;b] аралығындағы анықталған интегралы деп аталады және
жағдайдағы шегі функцияның [a;b] аралығындағы анықталған интегралы деп аталады және  деп белгіленеді. Сонымен,
деп белгіленеді. Сонымен, 
 , (2)мұндағы а және b сандары интегралдың сәйкес төменгі және жоғарғы шектері деп аталады.
, (2)мұндағы а және b сандары интегралдың сәйкес төменгі және жоғарғы шектері деп аталады.
Белгіленуі мен айтылуында ұқсастық болғанымен анықталған және анықталмаған интеграл екеуі түрлі ұғымды береді: 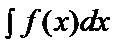 - функциялар жиыны болса;
- функциялар жиыны болса;  - нақтылы сан болады.
- нақтылы сан болады.
Егер [ a;b ] кесіндіде f(x)>0 болса, онда анықталған интеграл анықтамасынан оның геометриялық мағнасы шығады:  -үстіңгі жағынанy=f(x) қисығымен, бүйір жақтарынан x=a, x=b түзулерімен, астыңғы жағынан y=0 түзуімен шектелген қисық сызықты трапеция ауданы.
-үстіңгі жағынанy=f(x) қисығымен, бүйір жақтарынан x=a, x=b түзулерімен, астыңғы жағынан y=0 түзуімен шектелген қисық сызықты трапеция ауданы.
Анықталған интеграл қасиеттері. 1. Тұрақтыны шек таңбасы алдына шығаруға болады: 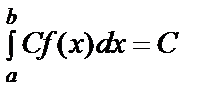
 .
.
2.Екі функцияның алгебралық қосындысының интегралы сол функциялар интегралдарының алгебралық қосындысына тең болады: 

 .
.
3Интеграл шектерінің орындарын ауыстырғанда интеграл таңбасы қарама-қарсыға өзгереді: 
 . Интеграл шектері бірдей болғанда интеграл мәні нолге тең:
. Интеграл шектері бірдей болғанда интеграл мәні нолге тең:  .
.
Tuth  ,jkcf? jylf m(b-a)<
,jkcf? jylf m(b-a)<  <M(b-a) / Егер с нүктесі [ a;b ] кесіндісінде жатқан нүкте болса, онда
<M(b-a) / Егер с нүктесі [ a;b ] кесіндісінде жатқан нүкте болса, онда 

 .
.
Орта мән туралы теорема. y=f(x) функциясы [ a;b ] кесіндісінде үзіліссіз функция болса, онда қандай да бір с  [ a;b ] нүкте табылады да мына теңдік орындалады:
[ a;b ] нүкте табылады да мына теңдік орындалады: 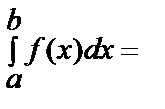 (b-a)f(c).
(b-a)f(c).
Егер y=f(x) функциясы жұп болса, онда  2
2  .
.
Егер y=f(x) функциясы тақ болса, онда  0
0
79. Анықталған интегралдың қолданылуы. Жазық фигураның ауданын табу.
а)  функциясы
функциясы  кесіндісінде теріс емес және үзіліссіз болсын. Онда жоғарыдан
кесіндісінде теріс емес және үзіліссіз болсын. Онда жоғарыдан  функциясының графигімен, төменнен
функциясының графигімен, төменнен 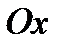 өсімен, ал бүйір жақтарынан
өсімен, ал бүйір жақтарынан  түзулерімен қоршалған қисық сызықты трапецияның ауданы
түзулерімен қоршалған қисық сызықты трапецияның ауданы  интегралына тең болады, яғни
интегралына тең болады, яғни  Егер
Егер  кесіндісінде
кесіндісінде  болса, онда қисық сызықты трапеция
болса, онда қисық сызықты трапеция 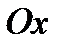 өсінің төменгі жағына орналасқан және
өсінің төменгі жағына орналасқан және  болады.
болады.
1-мысал.  синусоидасымен және
синусоидасымен және 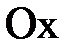 осімен шектелген фигураның ауданын табу керек (
осімен шектелген фигураның ауданын табу керек ( ).
).

|

|

|
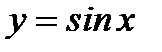
|

|

|
 аралығында
аралығында  , ал
, ал  аралығында
аралығында 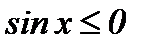 болғандықтан, берілген облыстың ауданын табайық
болғандықтан, берілген облыстың ауданын табайық

 .
.
б)  түзулерімен және
түзулерімен және  аралығында үзіліссіз
аралығында үзіліссіз 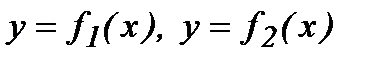 (мұндағы
(мұндағы 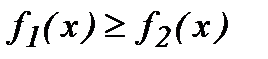 ) функциялардың графиктерімен шектелген фигураның ауданы мына формуламен табылады.
) функциялардың графиктерімен шектелген фигураның ауданы мына формуламен табылады. 
в) Егер 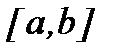 кесіндісінде
кесіндісінде  функциясының графигі параметрлік функция түрінде берілсін
функциясының графигі параметрлік функция түрінде берілсін  мұндағы
мұндағы  үзіліссіз, ал
үзіліссіз, ал  функциясы
функциясы 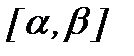 кесіндісінде бір сарынды, үзіліссіз дифференциалданатын функция, ал
кесіндісінде бір сарынды, үзіліссіз дифференциалданатын функция, ал  ,
,  болса, онда қисық сызықты трапецияның ауданы мына формуламен табылады
болса, онда қисық сызықты трапецияның ауданы мына формуламен табылады  .
.
2−мысал. Жарты өстері  және
және  болатын эллипстің жоғарғы жағындағы жарты бөлігінің параметрлік теңдеуі былай беріледі:
болатын эллипстің жоғарғы жағындағы жарты бөлігінің параметрлік теңдеуі былай беріледі:  . Егер
. Егер  десек, онда
десек, онда  , ал
, ал  десек
десек  тең болады. Сонда эллипстің ауданы былай табылады
тең болады. Сонда эллипстің ауданы былай табылады
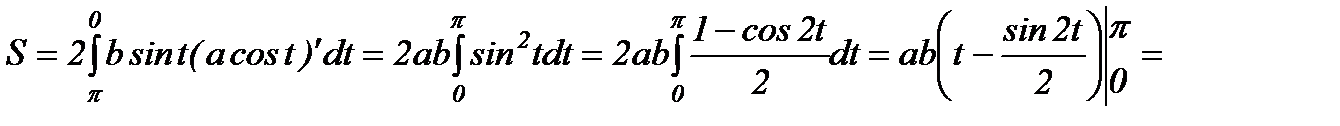
 . Поляр координаттарындағы аудан. Координат төбесінен шығатын сәулелермен
. Поляр координаттарындағы аудан. Координат төбесінен шығатын сәулелермен 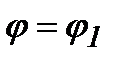 және
және  (мұндағы
(мұндағы  ) және теріс емес
) және теріс емес  функциясының
функциясының  кесіндідегі үзіліссіз графигімен шектелген қисықсызықты үшбұрыштың ауданы мына формуламен есептелінеді:
кесіндідегі үзіліссіз графигімен шектелген қисықсызықты үшбұрыштың ауданы мына формуламен есептелінеді: 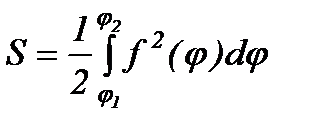
3-мысал.  қисығымен шенелген облыстың ауданын табамыз. Бұл қисық Бернулли лемнискатасы деп аталады.
қисығымен шенелген облыстың ауданын табамыз. Бұл қисық Бернулли лемнискатасы деп аталады.
 шартынан интегралдау
шартынан интегралдау
облысы табылады. Осыдан 
 үшін бүкіл облыстың
үшін бүкіл облыстың  -ін құрайды.
-ін құрайды.

 .
.
3. Қисық доғасының ұзындығы
а) Егер қисық декарт координаттар жүйесінде  ,
,  теңдеуімен берілсе, онда қисықтың доғасының ұзындығы мына формуламен есептелінеді:
теңдеуімен берілсе, онда қисықтың доғасының ұзындығы мына формуламен есептелінеді:  .
.
б) Егер қисық параметрлік түрде  берілсе, онда қисықтың доғасының ұзындығы мына формуламен есептелінеді:
берілсе, онда қисықтың доғасының ұзындығы мына формуламен есептелінеді:  .
.
в) Егер қисық сызық полярлық координаталар арқылы берілсе, яғни  (
( ), онда
), онда 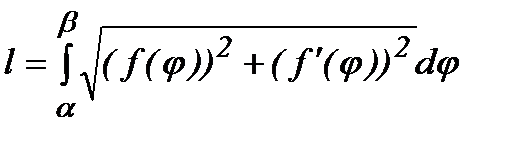 .
.
Айналу денесінің көлемі. Үзіліссіз  сызығымен және
сызығымен және  түзулерімен шектелген қисық сызықты трапеция
түзулерімен шектелген қисық сызықты трапеция  өсінен айналуынан пайда болған айналу денесінің көлемі мына формуламен есептелінеді:
өсінен айналуынан пайда болған айналу денесінің көлемі мына формуламен есептелінеді:  .
.
4-мысал. 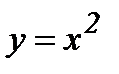 ,
, 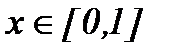 функциясының графигімен берілген қисық сызықты трапецияның
функциясының графигімен берілген қисық сызықты трапецияның  өсінен айналуынан пайда болған дененің көлемін табу керек. Жоғарыдағы формуланы қолданамыз
өсінен айналуынан пайда болған дененің көлемін табу керек. Жоғарыдағы формуланы қолданамыз  .
.
Айналу бетінің ауданын табу. Айталық, үзіліссіз дифференциалданатын  , (
, ( және
және 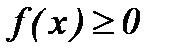 ) функциясының графигі
) функциясының графигі  өсінен айналсын. Пайда болған айналу бетінің ауданы:
өсінен айналсын. Пайда болған айналу бетінің ауданы:
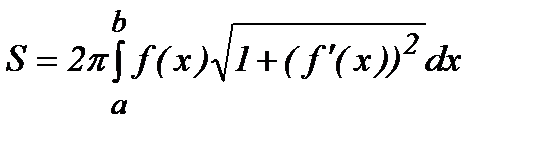
80. Меншіксіз интегралдар. Анықталған интегралды қарастырғанда интегралдың төменгі және жоғары шектері – ақырлы сандар және интеграл астындағы функция –интегралдау аралығында ақырлы функция болуын талап еттік. Егер осы қойылған шарттардың біреуі орындалмаса, интеграл меншіксіз интеграл деп аталады.
1. Ақырсыз шектері бар меншіксіз интегралдар. Айталық,  функциясы
функциясы  аралығында үзіліссіз болсын. Осы функциядан
аралығында үзіліссіз болсын. Осы функциядан  -дан
-дан 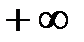 дейін алынған меншіксіз интеграл деп мына шекті айтамыз:
дейін алынған меншіксіз интеграл деп мына шекті айтамыз:  . Егер осы шек бар (санға тең) болса, онда меншіксіз интегралы жинақты, ал шегі жоқ немесе шексіздікке тең болса, онда интеграл жинақсыз деп аталады. Егер
. Егер осы шек бар (санға тең) болса, онда меншіксіз интегралы жинақты, ал шегі жоқ немесе шексіздікке тең болса, онда интеграл жинақсыз деп аталады. Егер  аралығында
аралығында  болса, онда мұндай интеграл шекаралары:
болса, онда мұндай интеграл шекаралары:  ,
, 
 түзулерімен және
түзулерімен және  функциясының графигімен шектелген фигураның ауданын береді. Жинақты интеграл үшін бұл аудан шектеулі, ал жинақсыз интеграл үшін шектеусіз болады.
функциясының графигімен шектелген фигураның ауданын береді. Жинақты интеграл үшін бұл аудан шектеулі, ал жинақсыз интеграл үшін шектеусіз болады.
5-мысал.  . Демек, интеграл жинақсыз.
. Демек, интеграл жинақсыз.
Айталық,  функциясы
функциясы  аралығында үзіліссіз болсын. Сонда
аралығында үзіліссіз болсын. Сонда  -тен
-тен  -ға дейінгі меншіксіз интеграл деп мына шекті айтамыз
-ға дейінгі меншіксіз интеграл деп мына шекті айтамыз  .
.
Мұндай интеграл ( болғанда) шекаралары
болғанда) шекаралары  ,
, 
 және
және  болған фигураның ауданын өрнектейді.
болған фигураның ауданын өрнектейді.
Егер  функциясы бүкіл сандар осінде үзіліссіз болса, онда
функциясы бүкіл сандар осінде үзіліссіз болса, онда  -тен
-тен 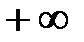 -ке дейінгі меншіксіз интеграл деп мына екі интегралдың қосындысын айтамыз
-ке дейінгі меншіксіз интеграл деп мына екі интегралдың қосындысын айтамыз
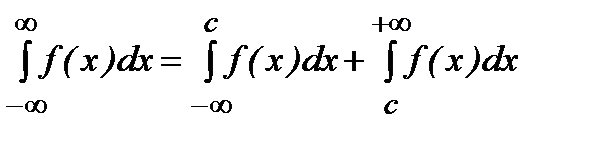
(мұнда 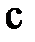 -кезкелгенсан). Бұланықтама
-кезкелгенсан). Бұланықтама 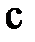 -нытаңдапалуғабайланыссыз. Мұндағы екі интеграл да жинақты болса, онда ол интеграл жинақты деп аталады.
-нытаңдапалуғабайланыссыз. Мұндағы екі интеграл да жинақты болса, онда ол интеграл жинақты деп аталады. 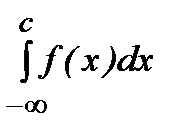 және
және  . Егер осы интегралдың біреуі жинақсыз болса, онда
. Егер осы интегралдың біреуі жинақсыз болса, онда  интегралы жинақсыз деп аталады.
интегралы жинақсыз деп аталады.
Не нашли, что искали? Воспользуйтесь поиском: