
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Коллинеар векторлар. 9 страница. Мұндағы қатынасты шектер тілінде “ақырсыз азға кері шама ақырсыз үлкен” дейді де
Мұндағы 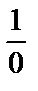 қатынасты шектер тілінде “ақырсыз азға кері шама ақырсыз үлкен” дейді де, шексіздікке теңестіреді.
қатынасты шектер тілінде “ақырсыз азға кері шама ақырсыз үлкен” дейді де, шексіздікке теңестіреді.
Ақырсыз аз функциялар нолге әртүрлі жылдамдықпен жақындайды. Көптеген жағдайда ақырсыз аздардың нолге ұмтылу жылдамдығын анықтау үшін оларды өзара салыстыру керек болады. Салыстыру үшін олардың қатынасының  жағдайдағы шегін қарастырады.
жағдайдағы шегін қарастырады.
Ақырсыз аздарды салыстыру
Айталық 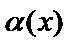 және
және 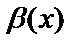
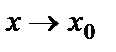 жағдайда ақырсыз аз функциялар және
жағдайда ақырсыз аз функциялар және 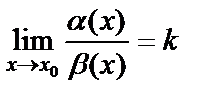 болсын. Онда, егер
болсын. Онда, егер
1) 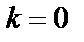 болса
болса 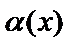
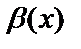 -ға қарағанда жоғары ретті ақырсыз аз деп;
-ға қарағанда жоғары ретті ақырсыз аз деп;
2) 
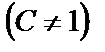 болса
болса  мен
мен  бірдей ретті ақырсыз аз деп;
бірдей ретті ақырсыз аз деп;
3) 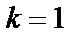 болса
болса 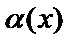 мен
мен  эквивалентті ақырсыз аз деп
эквивалентті ақырсыз аз деп
аталады. 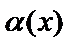 мен
мен 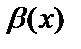 эквивалентті дегенді
эквивалентті дегенді 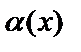 ~
~ 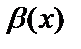 депжазады.
депжазады.
Егер 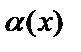 функциясы
функциясы  жағдайда ақырсыз аз болса, онда
жағдайда ақырсыз аз болса, онда
1. 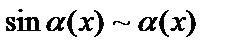 ,
,
 ,
,
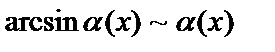 ,
,  ;
;
2.  ,
, 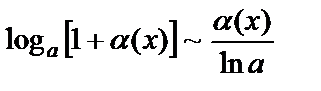 ;
;
3. 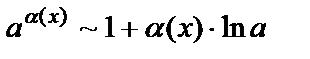 ,
,  ;
;
4. 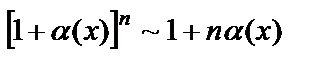 ,
, 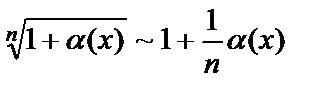 ;
;
5. 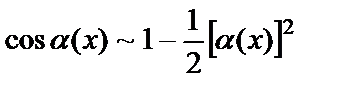 .
.
1.-5. қатынастар эквивалентті функциялар кестесін береді. Бұл кестені шек есептеу кезінде мына теоремаға сүйеніп қолдануға болады.
Теорема. Егер 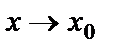 жағдайда
жағдайда 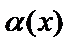 ~
~  және
және 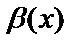 ~
~  болса, онда
болса, онда 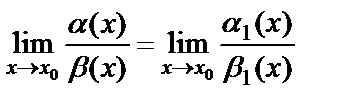 .
.
Мысал. 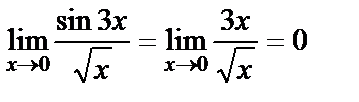 . Мұнда
. Мұнда 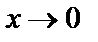 жағдайда
жағдайда 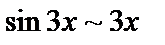 болғандықтан
болғандықтан  орнына
орнына 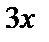 алынды.
алынды.
64. Шектер туралы негізгі теоремалар. Шек ұғымы, біржақты шектер
Анықтама. Егер алдын ала берілген, мейілінше аз 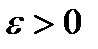 санына
санына 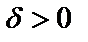 саны табылып,
саны табылып, 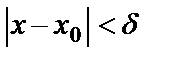 шартын қанағаттандыратын барлық х үшін
шартын қанағаттандыратын барлық х үшін  теңсіздігі орындалса, онда А саны f(x) функциясының х аргумент х0-ге ұмтылғандағы шегі деп аталады да, былай жазылады:
теңсіздігі орындалса, онда А саны f(x) функциясының х аргумент х0-ге ұмтылғандағы шегі деп аталады да, былай жазылады: 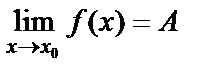 . Анықтамадағы
. Анықтамадағы  теңсіздікті ашсақ, мынадай қос теңсіздік аламыз:
теңсіздікті ашсақ, мынадай қос теңсіздік аламыз: 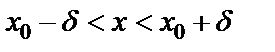 .
. 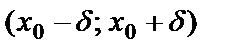 интервалды
интервалды  нүктесінің
нүктесінің  -маңайы дейді. Сол сияқты
-маңайы дейді. Сол сияқты 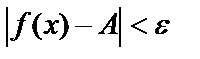 теңсіздікті ашсақ:
теңсіздікті ашсақ: 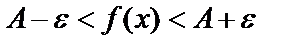 .
. 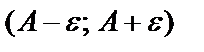 интервалды А нүктесінің
интервалды А нүктесінің 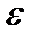 -маңайы дейді.
-маңайы дейді.
y
А+  y=f(x)
A
s c1BLAQItABQABgAIAAAAIQCt1jxQCwMAAJIGAAAOAAAAAAAAAAAAAAAAAC4CAABkcnMvZTJvRG9j LnhtbFBLAQItABQABgAIAAAAIQDrcxdj3AAAAAkBAAAPAAAAAAAAAAAAAAAAAGUFAABkcnMvZG93 bnJldi54bWxQSwUGAAAAAAQABADzAAAAbgYAAAAA " path="m,1230l,e" filled="f">
A+
y=f(x)
A
s c1BLAQItABQABgAIAAAAIQCt1jxQCwMAAJIGAAAOAAAAAAAAAAAAAAAAAC4CAABkcnMvZTJvRG9j LnhtbFBLAQItABQABgAIAAAAIQDrcxdj3AAAAAkBAAAPAAAAAAAAAAAAAAAAAGUFAABkcnMvZG93 bnJldi54bWxQSwUGAAAAAAQABADzAAAAbgYAAAAA " path="m,1230l,e" filled="f">
A+  0 x0-
0 x0-  x0 х0 + x0 х0 + 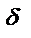 x x
|
Енді анықтаманы сурет бойынша айтсақ: Алдын ала берілген,  санына
санына 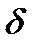 саны табылып, аргумент мәндері
саны табылып, аргумент мәндері  нүктесінің
нүктесінің  -маңайына тиісті болғанда функцияның сәйкес мәндері А нүктесінің
-маңайына тиісті болғанда функцияның сәйкес мәндері А нүктесінің 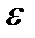 -маңайында жатса, А саны f(x) функциясының х аргумент х0 -ге ұмтылғандағы шегі деп аталады.
-маңайында жатса, А саны f(x) функциясының х аргумент х0 -ге ұмтылғандағы шегі деп аталады.
Мысал. Өндіріс орны шығаратын заттың бір данасының бағасы y пен оған деген сұраныс x (мың дана) арасындағы байланыс мынадай қатынаспен анықталған:
 .
.
| у 210 200 190 0 11,4 12 12,6 х |
Шешуі. (190; 210) интервалының ортасы А=200 теңге, олай болса  = 10. Шек анықтамасындағы
= 10. Шек анықтамасындағы 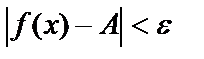 теңсіздігін қолданайық:
теңсіздігін қолданайық: 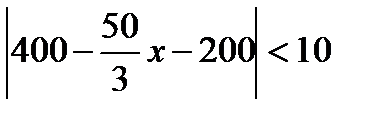 . Осы теңсіздікті түрлендіріп ықшамдасақ мынадай теңсіздік аламыз:
. Осы теңсіздікті түрлендіріп ықшамдасақ мынадай теңсіздік аламыз: 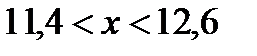 .
.
Соңғы теңсіздікті мынадай 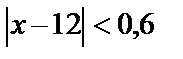 түрге келтіріп жазсақ, есеп сұрағына жауап беруге болады: Заттың бір данасының бағасының 200 теңгеден ауытқуы 10 теңгеден артпауы үшін, өндіріс орны өнім көлемінің өзгеруін 0,6 мың данадан асырмауы керек екен.
түрге келтіріп жазсақ, есеп сұрағына жауап беруге болады: Заттың бір данасының бағасының 200 теңгеден ауытқуы 10 теңгеден артпауы үшін, өндіріс орны өнім көлемінің өзгеруін 0,6 мың данадан асырмауы керек екен.
Айталық 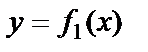 және
және  функцияларының
функцияларының 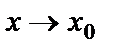 жағдайда
жағдайда  және
және 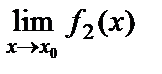 шектері бар болсын.
шектері бар болсын.
7. Екі функцияның алгебралық қосындысының шегі шектердің алгебралық қосындысына тең болады, яғни
8. 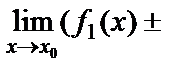
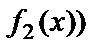 =
= 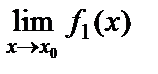
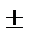
 .
.
9. Екі функцияның көбейтіндісінің шегі шектердің көбейтіндісіне тең болады, яғни
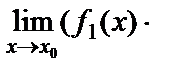
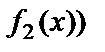 =
= 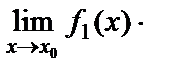
 .
.
Салдар. 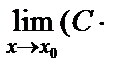
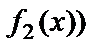 = С
= С  , мұндағы С - const.
, мұндағы С - const.
10. Екі функцияның қатынасының шегі шектердің қатынасына тең болады (әрине, егер бөлімдегі функция нолден өзгеше болса), яғни 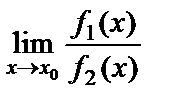 =
= 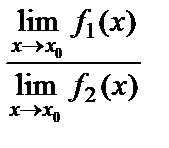 .
.
11. Мысал. 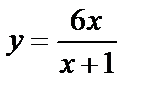 функциясының
функциясының  жағдайдағы шегін табу керек.
жағдайдағы шегін табу керек.
12. Шешуі. Қысқаша айтсақ 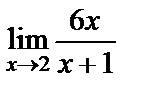 шек есептеу керек. Функция шегінің қасиеттерін қолданып есептейік:
шек есептеу керек. Функция шегінің қасиеттерін қолданып есептейік: 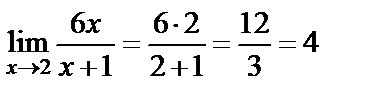 .
. 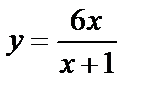 функциясының
функциясының  жағдайдағы шегі 4 болады екен.
жағдайдағы шегі 4 болады екен.
41-сурак1-ші тамаша шек
Теорема. 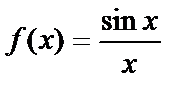 функциясы x=0 нүктеде анықталмаған, бірақ
функциясы x=0 нүктеде анықталмаған, бірақ  жағдайда шегі бар және
жағдайда шегі бар және 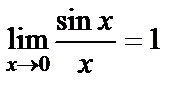 Осы шекті бірінші тамаша шек деп атайды.
Осы шекті бірінші тамаша шек деп атайды.
42-суракБірінші тамаша шек салдары:
1)  ,
,
2) 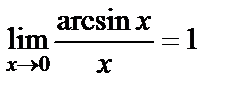 ,
,
3) 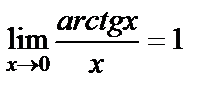 .
.
Мысал. а)  .
.
б) 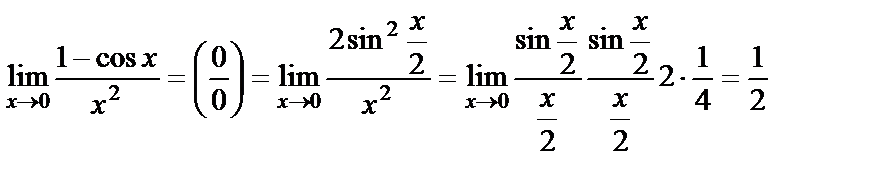 .
.
43-сурак Екінші тамаша шек
Теорема.  функциясының
функциясының  жағдайда шегі бар және
жағдайда шегі бар және 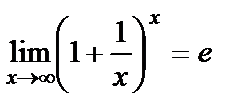
Осы шекті екінші тамаша шек деп атайды. Мұндағы 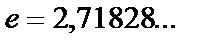 иррационал саны Эйлер саны екені белгілі.
иррационал саны Эйлер саны екені белгілі.
65. Бірінші және екінші тамаша шектер. Теорема. 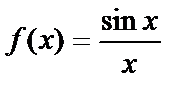 функциясы x=0 нүктеде анықталмаған, бірақ
функциясы x=0 нүктеде анықталмаған, бірақ  жағдайда шегі бар және
жағдайда шегі бар және 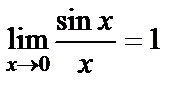 Осы шекті бірінші тамаша шек деп атайды.
Осы шекті бірінші тамаша шек деп атайды.
1)  ,
,
2) 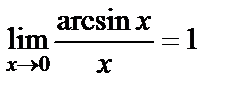 ,
,
3) 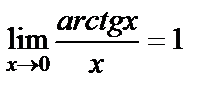 .
.
Мысал.
а)  .
.
б) 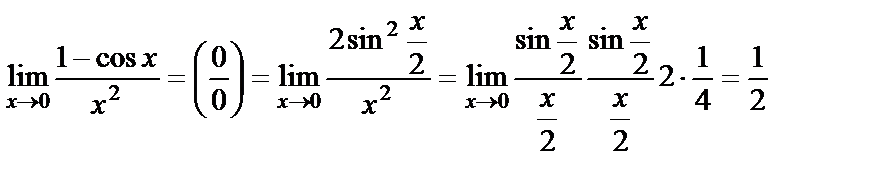 .
.
Теорема.  функциясының
функциясының  жағдайда шегі бар және
жағдайда шегі бар және 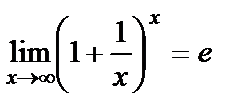
Осы шекті екінші тамаша шек деп атайды. Мұндағы 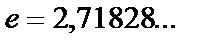 иррационал саны Эйлер саны екені белгілі. 1)
иррационал саны Эйлер саны екені белгілі. 1)  , a=e болғанда
, a=e болғанда 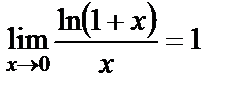 ;
;
2)  , a=e болғанда
, a=e болғанда 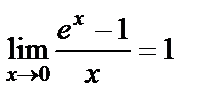 ;
;
3) 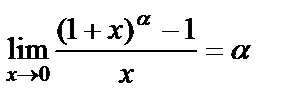 Мысал. а)
Мысал. а) 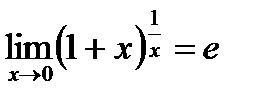 екенін көрсет
екенін көрсет
Шешуі. 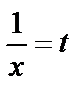 деген білгілеу енгізейік. Осыдан
деген білгілеу енгізейік. Осыдан 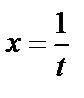 . Және де
. Және де  кезде
кезде  . Енді шек есептесек
. Енді шек есептесек 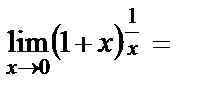
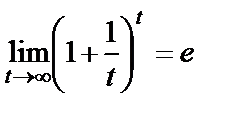 . б)
. б) 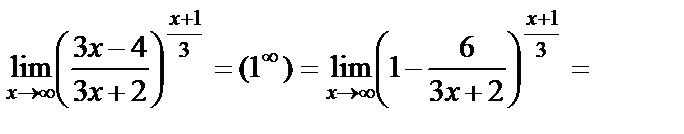
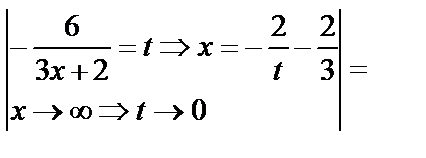
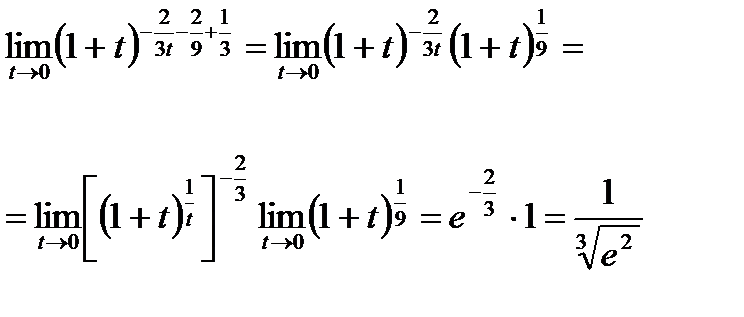
66. Функцияның үзіліссіздігі. Үзілу нүктелерінің түрлері. Анықтама. 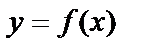 функциясының
функциясының 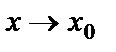 жағдайда шегі функцияның сол нүктедегі мәніне тең болса, яғни
жағдайда шегі функцияның сол нүктедегі мәніне тең болса, яғни  , функция
, функция  нүктесіндеүзіліссіз деп аталады.
нүктесіндеүзіліссіз деп аталады.
Егер 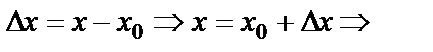

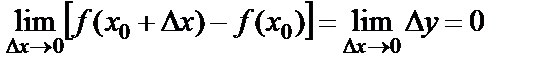 .
.
Сонда функция үзіліссіздігінің анықтамасын былай да айтуға болады: Берілген нүктеде аргументтің ақырсыз аз өсімшесіне функцияның да ақырсыз аз өсімшесі сәйкес келсе, яғни
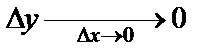 функция
функция 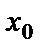 нүктесінде үзіліссіз деп аталады.
нүктесінде үзіліссіз деп аталады. 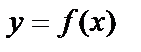 функциясы қандай да бір аралықтың үзіліссіз болуы үшін, ол сол аралықтың әрбір нүктесінде үзіліссіз болуы керек.
функциясы қандай да бір аралықтың үзіліссіз болуы үшін, ол сол аралықтың әрбір нүктесінде үзіліссіз болуы керек.
Үзіліссіз функция қасиеттері.
1. 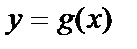 функциясы
функциясы  нүктесінде үзіліссіз, ал
нүктесінде үзіліссіз, ал 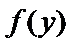 функциясы
функциясы  нүктесінде үзіліссіз болса,
нүктесінде үзіліссіз болса, 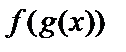 күрделі функциясы
күрделі функциясы 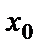 нүктесінде үзіліссіз болады және
нүктесінде үзіліссіз болады және 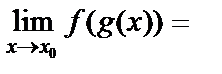
 .
.
2. Нүктеде үзіліссіз функциялардың алгебралық қосындысы, көбейтіндісі және қатынасы (бөліміндегі функция нолден өзге болғанда) үзіліссіз функция болады
Анықтама. 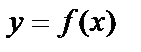 функциясының
функциясының 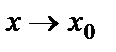 жағдайда шегі функцияның сол нүктедегі мәніне тең болмаса, яғни
жағдайда шегі функцияның сол нүктедегі мәніне тең болмаса, яғни 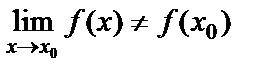 , функция
, функция 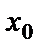 нүктесінде үзілісті функция деп, ал
нүктесінде үзілісті функция деп, ал 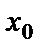 нүктені функцияның үзіліс нүктесі деп атайды. Біржақты шектер ұғымын енгізейік.
нүктені функцияның үзіліс нүктесі деп атайды. Біржақты шектер ұғымын енгізейік.
Айталық  және
және 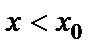 , онда
, онда 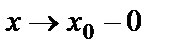 деп жазады, ал осы жағдайдағы
деп жазады, ал осы жағдайдағы 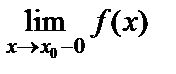 шекті функцияның сол жақты шегі деп атайды. Дәл осылайша функцияның оң жақты
шекті функцияның сол жақты шегі деп атайды. Дәл осылайша функцияның оң жақты 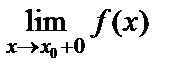 шегі де анықталады. Функцияның сол жақты және оң жақты шектерін біржақты шектер дейді.
шегі де анықталады. Функцияның сол жақты және оң жақты шектерін біржақты шектер дейді.
Анықтама. Функцияның 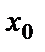 нүктесінде өзара тең емес ақырлы біржақты шектері бар болса,
нүктесінде өзара тең емес ақырлы біржақты шектері бар болса, 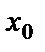 нүктесі функцияның І-текті үзіліс нүктесі деп аталады. Кейде оны ақырлы секіріс деп (10а-сурет) атайды.
нүктесі функцияның І-текті үзіліс нүктесі деп аталады. Кейде оны ақырлы секіріс деп (10а-сурет) атайды.
Анықтама. Функцияның  нүктесіндегі ақырлы біржақты шектердің ең болмағанда біреуі жоқ болса,
нүктесіндегі ақырлы біржақты шектердің ең болмағанда біреуі жоқ болса, 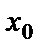 нүктесі функцияның ІІ-текті үзіліс нүктесі деп аталады
нүктесі функцияның ІІ-текті үзіліс нүктесі деп аталады
Мысал. а) 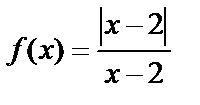 функциясы
функциясы  нүктесінде үзіліссіздікке зертте.
нүктесінде үзіліссіздікке зертте.
Шешуі. 
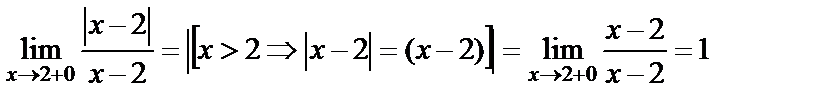 ,
,
яғни сол жақты шегі –1, ал оң жақты шегі 1, ақырлы сандар, өз-ара тең емес, олай болса 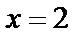 нүктесі І-текті үзіліс нүктесі болады.
нүктесі І-текті үзіліс нүктесі болады.
б) 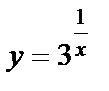 функциясын үзіліссіздікке зертте.
функциясын үзіліссіздікке зертте.
Шешуі. Функция 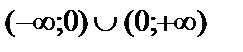 аралығында анықталған.
аралығында анықталған.  нүктесіндегі біржақты шектерді табайық.
нүктесіндегі біржақты шектерді табайық.

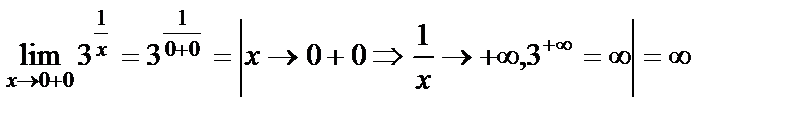 ,
,
яғни сол жақты шегі 0, ал оң жақты шегі шексіздік. Олай болса 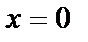 нүктесі ІІ-текті үзіліс нүктесі болады (10б-сурет).
нүктесі ІІ-текті үзіліс нүктесі болады (10б-сурет).
в) 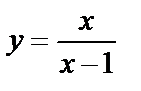 функциясын үзіліссіздікке зертте.
функциясын үзіліссіздікке зертте.
| 0 x0 ← x0+Δx x |
 
|
| Δx |
| Δy |
| y |
| 3-сурет |
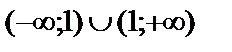 аралығында анықталған.
аралығында анықталған. 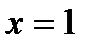 нүктесіндегі біржақты шектерді табайық.
нүктесіндегі біржақты шектерді табайық.
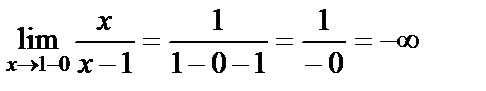
 ,
,
яғни сол жақты де, оң жақты шегі де шексіздік. Олай болса 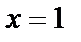 нүктесі ІІ-текті үзіліс нүктесі болады
нүктесі ІІ-текті үзіліс нүктесі болады
| 0 1 x |
| y |
| 0 x |
| y |
| -1 |
| 0 2 x |
| y |
67. Функцияның туындысы. Функция туындысы
Көп жағдайда функция мәнін білумен қатар аргументтің өзгерісіне байланысты функцияның өзгеру жылдамдығын білу де маңызды болады.y =f(x) функциясын қарастырайық (1-сурет). Осы функция  кесіндісінде анықталған және үзіліссіз болсын. Кез келген
кесіндісінде анықталған және үзіліссіз болсын. Кез келген 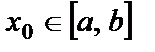 үшін
үшін  айырма х аргументтің
айырма х аргументтің 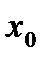 нүктесіндегі өсімшесі деп аталады да,
нүктесіндегі өсімшесі деп аталады да,  деп белгіленеді. Сонымен,
деп белгіленеді. Сонымен, 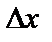 =
=  x =
x = 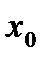 +
+ 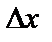 . Ал
. Ал  айырма f(x) функциясының
айырма f(x) функциясының 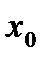 нүктесіндегі өсімшесі деп аталады да,
нүктесіндегі өсімшесі деп аталады да, 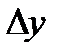 деп белгіленеді. Сонымен,
деп белгіленеді. Сонымен,  =
=  =
= 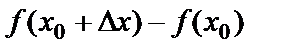 .
.
2-суретте көрсетілген y=f1(x) және y=f2(x) функцияларды қарастырайық. Аргумент мәні  шамаға өзгергенде бұл функциялардың мәндері де белгілі бір шамаға өзгереді. Суретте f2(x) функцияның мәні f1(x) функцияға қарағанда көп өзгереді (өседі).
шамаға өзгергенде бұл функциялардың мәндері де белгілі бір шамаға өзгереді. Суретте f2(x) функцияның мәні f1(x) функцияға қарағанда көп өзгереді (өседі).
Аргумент мәні бірдей шамаға өзгерген кездегі функциялардың өзгерістерін салыстыру үшін функцияның өзгеріс жылдамдығы ұғымын енгізеді. Оны орташа жылдамдық дейді де, функция өзгерісінің аргумент өзгерісіне қатынасымен анықтайды:
Орташа жылдамдық х0 нүктесіне ғана қатысты қарастырылмай, аргумент өзгерісінен де байланысты болады. Функция жылдамдығын аргумент өзгерісінен байланыссыз қарастыру үшін функцияның нүктедегі жылдамдығын қарастырады. Функцияның нүктедегі жылдамдығын анықтау үшін х -ті х0 аргументке шексіз жақындатады, немесе  . Осы кезде үзіліссіз функция өзгерісі нолге жақындайды, яғни
. Осы кезде үзіліссіз функция өзгерісі нолге жақындайды, яғни 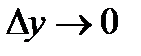 . Нолге шексіз жақындайтын функция өзгерісінің нолге шексіз жақындайтын аргумент өзгерісіне қатынасы функцияның х0 нүктедегі өзгеріс жылдамдығын береді. Функцияның х0 нүктедегі осы өзгеріс жылдамдығын f(x) функциясының х0 нүктедегі туындысы деп атайды:
. Нолге шексіз жақындайтын функция өзгерісінің нолге шексіз жақындайтын аргумент өзгерісіне қатынасы функцияның х0 нүктедегі өзгеріс жылдамдығын береді. Функцияның х0 нүктедегі осы өзгеріс жылдамдығын f(x) функциясының х0 нүктедегі туындысы деп атайды:
Не нашли, что искали? Воспользуйтесь поиском: