Коллинеар векторлар. 5 страница

33. Вектордың бағыттаушы косинустары. Бағыттаушы косинустар - 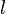түзуінің бағыттаушыкосинустар деп осы түзудің бағыттауышы векторы 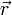-дің 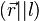Ох,Оу,Оз координат өстерінің оң бағытымен жасайтын α, β, γ бұрыштарының косинусын атайды. Бағыттаушы косинустар өзара теңдігімен байланысады. Бағыттаушы косинустар осы бағыттағыбірлік векторлардың координаттары болады. 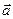векторы мен бірлік векторларының арасындағы бұрыштарды қарастырамыз. Ол бұрыштарды былай белгілейік:

; ;

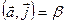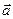векторының кез келген бірлік векторға, мысалы i-ге, көбейтіндісін қарастырамыз: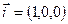

Бұдан (*) формуласы бойынша бұрышының косинусын табамыз:

Осы тәсілменқалғанбұрыштардыңкосинусынтабамыз:

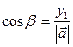; (8)

Бұлкосинустар 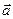векторыныңбағыттаушыкосинустарыдепаталады. Бағыттаушыкосинустардыңквадраттарыныңқосындысыбіргетең:

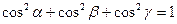
Бұлформуланыдәлелдеуүшін (8) формуланы квадрат дәрежегешығарамыз да қосамыз.

3-мысал.

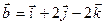және векторлары -ныңқандаймәнінде перпендикуляр болады. (7) перпендикулярлықшартыбойыншаолардыңскалярлықкөбейтіндісінтабамыз:

; 1*2-3*2-2*2=0; =10.

4-мысал.

және векторларыберілсінделік.

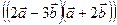скалярлықкөбейтіндісінесептеукерек.

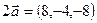
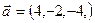
-3 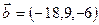2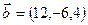

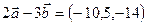
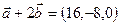
Еківектордыңізделінді скаляр көбейтіндісінтабайық.

Вектордыңөзініңөзінескалярлықкөбейтіндісіоныңұзындығыныңквадратынатеңболады:

Вектордыңбағыты.

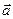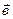, векторларыберілсін. Осы векторлардыңарасындағыбұрыштыанықтаукерек.

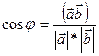Скалярлықкөбейтінді формуласынан (*) аламыз.

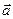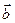О-дікемес және векторлардыңарасындағыбұрыштың косинусы осы векторлардыңскалярлықкөбейтіндісін, олардыңұзындықтарыныңкөбейтіндісінебөлгенгетең.

Ал вектордыңкоординаттарыберілсе, онда

(**)

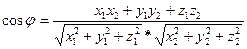1-мысал.

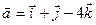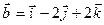; векторларыныңарасындағы 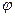бұрышын табу керек. (**) - формуласынпайдаланамыз.

Начало формы

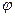; =135⁰.

1-мысал. Егер 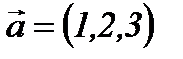, онда Егер векторы Ох, Оу, Oz өстерімен сәйкесінше бұрыштарын құрса, онда

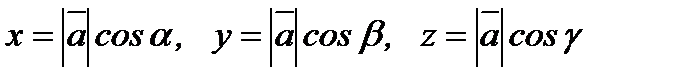, осыдан 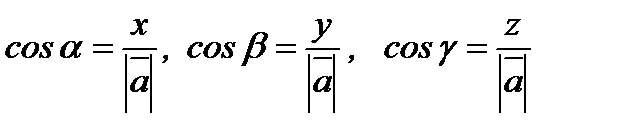болады.

Мұндағы сандары 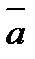векторының бағыттаушы косинустары деп аталады. Алдыңғы өрнекті вектордың модулінің формуласына қойып,

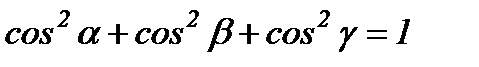теңдігін аламыз. бірлік векторының коодинаттары 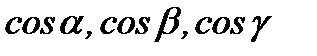екенін оңай байқауға болады. Сонымен, .

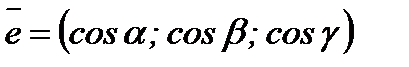2-мысал. 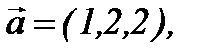векторы үшін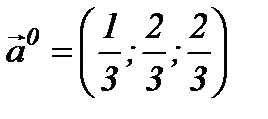

34. Координаттарымен берілген векторларға амалдар қолдану. Координаттарымен берілген векторларға амалдар қолдану

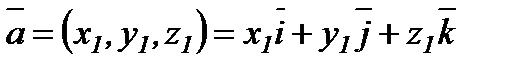, болса,

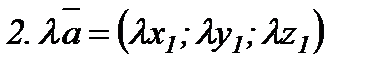
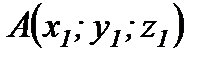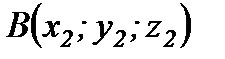35. Кесіндіні берілген қатынаста бөлу формулалары. Кесіндіні берілген қатынаста бөлу. және нүктелері арқылы өтетін кесінді берілсін. Осы кесіндіні 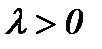қатынасындай етіп бөлетін 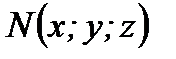нүктесінің координаттары: , , 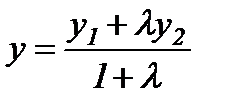- кесіндіні берілген қатынаста бөлу формулаларымен анықталады. Егер 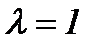болса, яғни 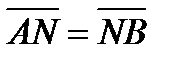онда

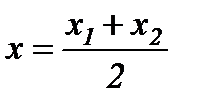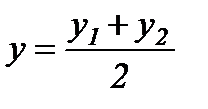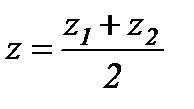, , - кесіндінің ортасын табу формуласы.

 

36. Кесіндінің ортасын табу формуласы.

Жазықтықта 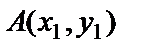және 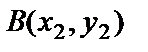екі нүкте берілсін. АВ кесіндісін АМ:МВ= 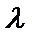болатындай қатынаспен бөлетін М(х,у) нүктесінің координаталары мынадай формуламен есептелінеді:

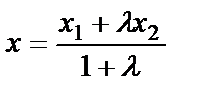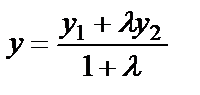, . Дербес жағдайда, АВ кесіндісін тең екіге бөлу керек болса, яғни =1:1=1, формула былай түрленеді: 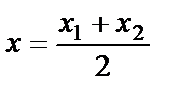, 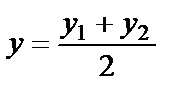.Егер 1 болса, яғни AN  NB онда

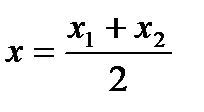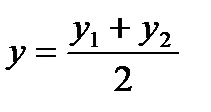; ; - кесіндінің ортасын табу формуласы.

37. Векторлардың скалярлық көбейтіндісі. Екі вектордың скаляр көбейтіндісі деп осы векторлардың ұзындықтары мен олардың арасындағы бұрыштың косинусына көбейтіндісіне тең шаманы айтады: .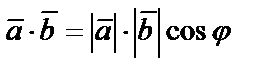

A

y2   y1

0 x1x2 x

B

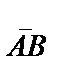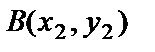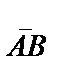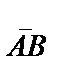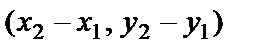
Тік бұрышты декарт координаталар жүйесінде векторының басы мен соңының координаталары белгілі болсын және . Сонда векторын координаталары арқылы былай жазуға болады: = 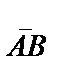векторының басы координаталар басымен беттесетіндей етіп өз-өзіне параллель көшірсек, онда 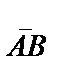векторының координатасы вектордың соңының координаталарымен бірдей болатынын аңғару қиын емес. Жазықтықта вектордың координатасын екі сан анықтаса, айталық , кеңістікте үш сан анытайды, .

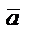
a 2 y

a1 x

z   a3

a 1 x

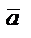
a2

y

Вектордың ұзындығы оның координаталарының квадраттарының қосындысынан алынған квадрат түбірге тең: 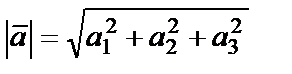. және векторлары координаталарымен берілген болса олардың қосындысы мынадай түрде анықталады: 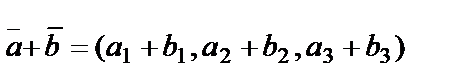.Ал векторын 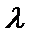санға көбейту мынадай түрде анықталады: 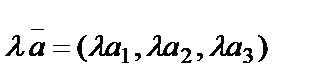. және векторларының скаляр көбейтіндісі мынадай:

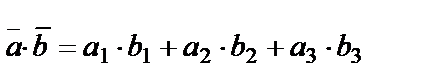
Анықтама. Екі 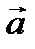және векторларының скалярлық көбейтіндісі деп 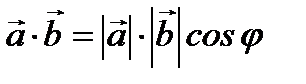санын айтады. Скаляр көбейтінді 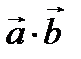, , 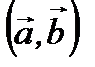символдармен белгіленеді. Мұндағы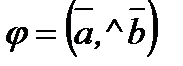 (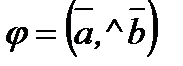), болғандықтан 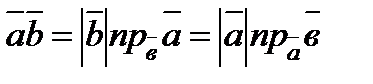деп жазуға болады.

4-мысал. Егер 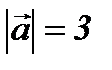, , 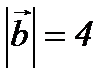, онда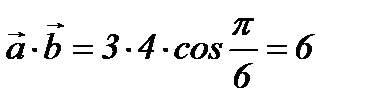

Теорема. 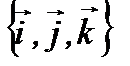базисінде 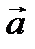векторының координаталары 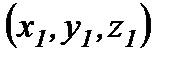, ал векторының координаталары 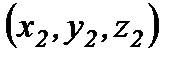болсын. Онда .

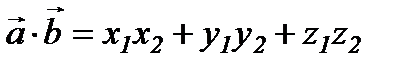5-мысал. Егер , болса, онда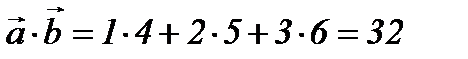

Скалярлық көбейтіндінің қолданылуы

1. 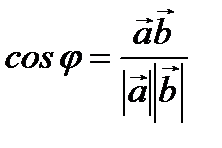немесе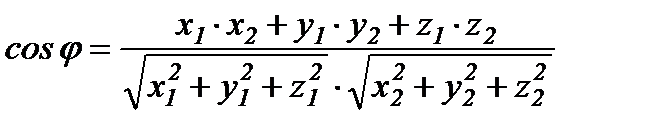

2.

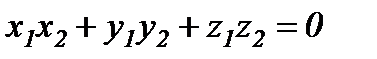
3. 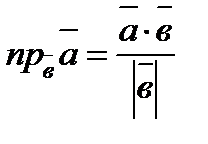(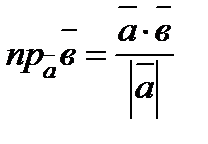) немесе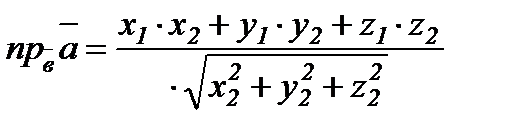

38. Векторлардың векторлық көбейтіндісі. Анықтама. және векторларының векторлық көбейтіндісі деп, келесі үш шартты қанағаттандыратын 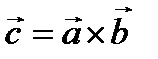векторын айтады:

1) ;

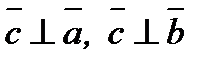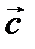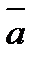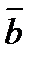2) векторының ұзындығы және векторларына тұрғызылған параллелограммның ауданына тең, яғни 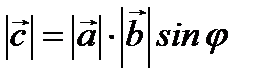, мұндағы ;

3) 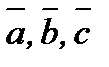векторлары оң үштік құрайды.

Векторлық көбейтінді 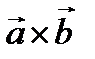немесе 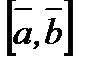деп белгіленеді.

Векторлық көбейтіндінің анықтамасынан , , 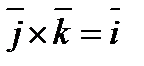болады

Векторлық көбейтіндінің қолданылуы

1. ,

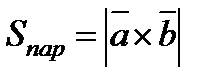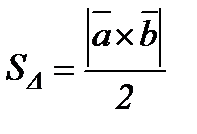
2. Егер 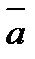|| 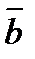болса, онда 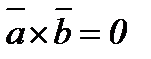(және керісінше)

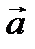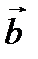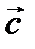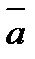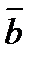39. Векторлардың аралас көбейтіндісі. Анықтама. , , векторларының аралас көбейтіндісі деп, және векторларының векторлық көбейтіндісі мен 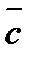векторының скаляр көбейтіндісін айтады.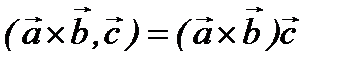

Аралас көбейтінді 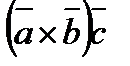не немесе түрінде жазылады. Аралас көбейтіндінің нәтижесі санға тең.

Аралас көбейтіндінің қасиеттері:

1. ;

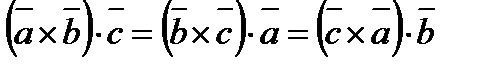2. ;

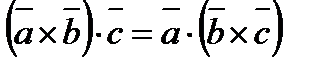3. ;

4. Егер векторлар 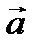, , 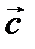компланар болса, онда .

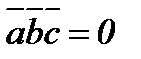Теорема. базисінде 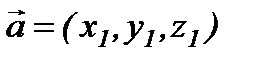, , 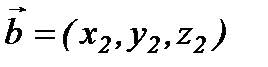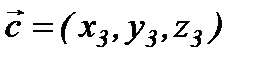векторлары берілсін, онда олардың аралас көбейтіндіні анықтауыш түрінде жазуға болады.

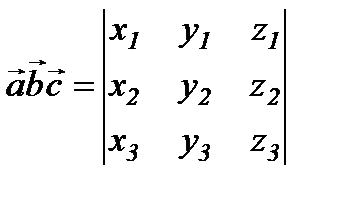
Аралас көбейтіндінің қолданылуы

1. Егер болса, онда 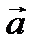, , 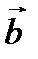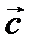-оң үштік; егер 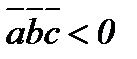болса, онда 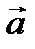, , - сол үштік құрайды.

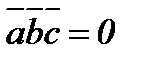
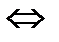
2. 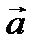, , 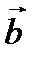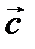векторлары компланар.

3. , .

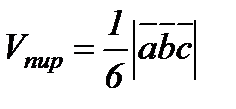40. Жазықтықтағы түзулердің әртүрлі теңдеулері. Жазықтықтағы түзудің теңдеулері

1. Берілген нүктеден берілген векторға перпендикуляр өтетін түзудің теңдеуі

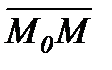Түзудің бойында жатқан нүктесі және оған перпендикуляр векторы берілген. Түзудің бойынан кез келген нүктесін аламыз. Сонда болады. векторы түзудің бойында жатқандықтан болады. Сондықтан олардың скалярлық көбейтіндісі , яғни

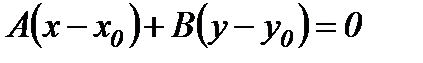(4.1)

Бұдан векторы түзуге перпендикуляр екендігі шығады. Түзуге перпендикуляр кез келген вектор түзудің нормалы немесе нормалдық векторы деп аталады.

2. Түзудің жалпы теңдеуі

(4.1) теңдеуінде жақшаларды ашып, 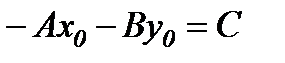деп белгілесек, түзудің жалпы теңдеуі шығады

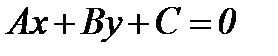(4.2)

Егер А=0 болса, онда түзу Ох өсіне параллель өтеді; егер В=0 болса, онда түзу Оу өсіне параллель өтеді; егер С=0 болса, онда түзу жүйенің бас нүктесі арқылы өтеді.

3. Түзудің бұрыштық коэффициент арқылы берілген теңдеуі. Егер 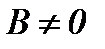болса, онда (4.2) теңдеуінен ()

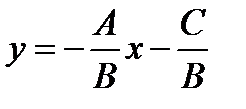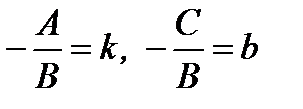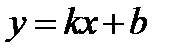
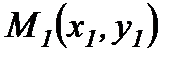4. Екі нүкте арқылы өтетін түзудің теңдеуі. Түзу және нүктелерінен өтсін. Түзудің бойынан кез келген нүктесін аламыз. Сонда бұл түзудің теңдеуі төмендегідей болады:

Не нашли, что искали? Воспользуйтесь поиском: