
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Коллинеар векторлар. 4 страница

|

|

|
Берілген а векторын кез келген k скалярға көбейту (бөлу) үшін осы вектордың модулін берілген санға көбейтеміз (бөлеміз): b = k • a (b = a:k). Қорытқы b вектордың бағыты k көбейткішінің (бөлгішінің) таңбасымен анықталады. Егер k оң болса (k > 0), онда b векторы а векторымен бағыттас, ал k теріс болса (k < 0), b векторының бағыты а векторының бағытына қарама-қарсы болады.Ұзындығы бірге тең векторды бірлік вектор деп атайды және оны е деп белгілейді. Егер бірлік векторының бағыты а векторының бағытымен сәйкес келсе онда ол а векторының орты деп аталады.
Коллинеар векторлар.
Басы А, соңы В нүктесі болатын бағытталған кесінді вектор деп аталады. Оқулықтарда векторларды  немесе
немесе 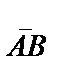 , кейде тек қалың әріптермен АВ белгілеу түрлері кездеседі. Сол сияқты векторларды бір әріппен де белгілей береді (
, кейде тек қалың әріптермен АВ белгілеу түрлері кездеседі. Сол сияқты векторларды бір әріппен де белгілей береді ( =
=  ,
,  , а).
, а).  векторының ұзындығы деп АВ кесіндісінің ұзындығын айтады және
векторының ұзындығы деп АВ кесіндісінің ұзындығын айтады және  деп белгілейді. Басы мен соңы беттесетін вектор нолдік вектор деп аталады,
деп белгілейді. Басы мен соңы беттесетін вектор нолдік вектор деп аталады,  =
=  және ұзындығы нолге тең.Бір түзудің не өзара параллель түзулер бойында орналасқан векторлар коллениар векторлар деп аталады.
және ұзындығы нолге тең.Бір түзудің не өзара параллель түзулер бойында орналасқан векторлар коллениар векторлар деп аталады.  және
және  векторларының қосындысы «үшбұрыш» не «параллелограмм» ережесімен анықталады:
векторларының қосындысы «үшбұрыш» не «параллелограмм» ережесімен анықталады:

|
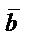
|

|

|

|

|
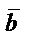
|

|
 және
және  векторларының
векторларының  -
-  айырымы деп
айырымы деп  -ға қосқанда
-ға қосқанда 

|

|

|
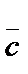 =
=  -
-  векторын айтады.
векторын айтады.
 ||
||  болғандықтан оны
болғандықтан оны  деп жазуға болады, мұндағы
деп жазуға болады, мұндағы  - қайсыбір сан. Осыдан
- қайсыбір сан. Осыдан 

 -екі вектордың коллинеарлығының белгісі.
-екі вектордың коллинеарлығының белгісі.
27. Компланар векторлар. Векторлардың компланарлық шарты а, в, с векторлардың бас нүктелерін бір нүктеге түйістіргенде олар бір жазықтықта орналасса онда ол векторлар компланар болады. Белгісі: а = в + с. Егер векторлар координаталарымен берілсе, яғни а (х1, у1, Z1), в (х2, у2, Z2), с (х3, у3, Z3) болса, онда олардың компланарлық белгісі:
х1 у1 Z1
х2 у2 Z2 = 0
х3 у3 Z3
Мысалдар: 1) а = i – j + 2, в= 3i +j,
c= mi + 2kвекторлары компланар болатындай m мәнін тап.
1 - 1 2
3 1 0 = 2 - 2m + 6 = 0 = m = 4, = а = gв + pс орындала ма, тексерейік; а (1; -1, 2) = g (3,
M0 2 1, 0) + р (4, 0, 2) = 1 = 3g + 4р
-1 = g + 0 =
2 = 0 + 2р
= g = -1 = а = -в + с, яғни векторлар компланар.
р = 1
Үш вектордың компланар бояу шарты
 (42)
(42)
формуламен, ал  векторлар қыры болатын параллепипед көлемi.
векторлар қыры болатын параллепипед көлемi.
 (43)
(43)
формуламен, ал бiр төбеден шығатын қырлары  болатын тетраэдрдiң көлемi.
болатын тетраэдрдiң көлемi.
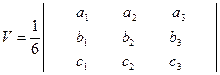 (44)
(44)
формуламен табылады.
28. Векторларға қолданылатын сызықтық амалдар. Векторларға қолданылатын сызықтық амалдар
Сызықтық амалдар деп, векторларды қосу және алу, векторды санға көбейту амалдарын айтады.Екі вектордың қосындысын екі жолмен табуға болады: бірі параллелограмм әдісі, екіншісі үшбұрыштар әдісі.
Параллелограмм әдісі.  және
және  векторларының қосындысы
векторларының қосындысы  деп,
деп,  және
және  векторларының ортақ бас нүктесінен шығатын, параллелограммның диагоналіне сәйкес келетін векторды айтады.
векторларының ортақ бас нүктесінен шығатын, параллелограммның диагоналіне сәйкес келетін векторды айтады.
Үшбұрыштар әдісі. Егер  векторының басы
векторының басы  векторының ұшына орналасса, онда
векторының ұшына орналасса, онда  және
және  векторларының қосындысы
векторларының қосындысы  деп,
деп,  векторының басы мен
векторының басы мен  векторының ұшын қосатын векторды айтады.
векторының ұшын қосатын векторды айтады.
Бір нүктеден шығатын  және
және  векторларының айырымы
векторларының айырымы  деп
деп  векторының ұшын
векторының ұшын  векторының ұшымен қосатын векторды айтады.
векторының ұшымен қосатын векторды айтады.
 векторының
векторының  санына көбейтіндісі деп ұзындығы
санына көбейтіндісі деп ұзындығы  -ға тең,
-ға тең,  векторына коллинеар, егер
векторына коллинеар, егер  болса
болса  векторымен бағыттас және
векторымен бағыттас және  болса,
болса,  векторына қарама-қарсы бағытталған
векторына қарама-қарсы бағытталған  векторын айтады.
векторын айтады.  және
және  векторларының коллинеарлығының қажетті және жеткілікті шарты:
векторларының коллинеарлығының қажетті және жеткілікті шарты: 
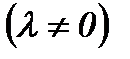
29. Векторлардың коллинеарлығының қажетті және жеткілікті шарттары.
Екі вектордың қосындысын екі жолмен табуға болады: бірі параллелограмм әдісі, екіншісі үшбұрыштар әдісі.
Параллелограмм әдісі.  және
және  векторларының қосындысы
векторларының қосындысы  деп,
деп,  және
және  векторларының ортақ бас нүктесінен шығатын, параллелограммның диагоналіне сәйкес келетін векторды айтады.
векторларының ортақ бас нүктесінен шығатын, параллелограммның диагоналіне сәйкес келетін векторды айтады.
Үшбұрыштар әдісі. Егер  векторының басы
векторының басы  векторының ұшына орналасса, онда
векторының ұшына орналасса, онда  және
және  векторларының қосындысы
векторларының қосындысы  деп,
деп,  векторының басы мен
векторының басы мен  векторының ұшын қосатын векторды айтады.
векторының ұшын қосатын векторды айтады.
Бір нүктеден шығатын  және
және  векторларының айырымы
векторларының айырымы  деп
деп  векторының ұшын
векторының ұшын  векторының ұшымен қосатын векторды айтады.
векторының ұшымен қосатын векторды айтады.
 векторының
векторының  санына көбейтіндісі деп ұзындығы
санына көбейтіндісі деп ұзындығы  -ға тең,
-ға тең,  векторына коллинеар, егер
векторына коллинеар, егер  болса
болса  векторымен бағыттас және
векторымен бағыттас және  болса,
болса,  векторына қарама-қарсы бағытталған
векторына қарама-қарсы бағытталған  векторын айтады.
векторын айтады.  және
және  векторларының коллинеарлығының қажетті және жеткілікті шарты:
векторларының коллинеарлығының қажетті және жеткілікті шарты: 
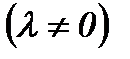
30. Сызықтық тәуелді және тәуелсіз векторлар. Векторлардың сызықтық тәуелділігі. Базис
 векторлар жүйесі берілсін.
векторлар жүйесі берілсін.
 векторлар жүйесі үшін бәрі бірдей нөлге тең емес және
векторлар жүйесі үшін бәрі бірдей нөлге тең емес және
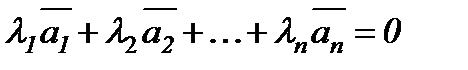
теңдігін қанағаттандыратын  сандары табылса, онда
сандары табылса, онда  векторларын сызықтық тәуелді векторлар деп атайды. Ал егер
векторларын сызықтық тәуелді векторлар деп атайды. Ал егер  теңдік тек
теңдік тек  сандарының барлығы бірдей нөлге тең болғанда ғана орындалса, онда
сандарының барлығы бірдей нөлге тең болғанда ғана орындалса, онда  векторлар жүйесі сызықтық тәуелсіз деп аталады.
векторлар жүйесі сызықтық тәуелсіз деп аталады.
Егер  теңдігі орындалатын
теңдігі орындалатын  сандары табылса, онда
сандары табылса, онда  векторы
векторы  векторларының сызықтық комбинациясы деп аталады.
векторларының сызықтық комбинациясы деп аталады.
31. Векторды координат өстердің орттары арқылы жіктеу. Кеңістіктегі тік бұрышты декарттық  координаталар жүйесін қарастырайық. Ох, Оу, Oz координат өстерінің бойында жатқан бірлік (орт) векторларды сәйкесінше
координаталар жүйесін қарастырайық. Ох, Оу, Oz координат өстерінің бойында жатқан бірлік (орт) векторларды сәйкесінше  деп белгілейік. Сонда реттелген үштік
деп белгілейік. Сонда реттелген үштік  кеңістікте базистік векторлар жүйесін құрайды. Мұндай, базистік векторлар жүйесін ортогональ базистік жүйе (базис) деп атайды
кеңістікте базистік векторлар жүйесін құрайды. Мұндай, базистік векторлар жүйесін ортогональ базистік жүйе (базис) деп атайды  .
. 
 , себебі үш вектордың қосындысы.
, себебі үш вектордың қосындысы.
Бұл формула  вектордың координат өстерінің орттары арқылы жіктелген түрі деп аталады немесе қысқаша
вектордың координат өстерінің орттары арқылы жіктелген түрі деп аталады немесе қысқаша  деп жазады.
деп жазады.
32. Вектордың модулі. Екінші жағынан  =
=  , Осыдан
, Осыдан  болғандықтан
болғандықтан  - вектордың модулі (ұзындығы).
- вектордың модулі (ұзындығы).
Басы А, соңы В нүктесі болатын бағытталған кесінді вектор деп аталады. Оқулықтарда векторларды  немесе
немесе 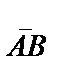 , кейде тек қалың әріптермен АВ белгілеу түрлері кездеседі. Сол сияқты векторларды бір әріппен де белгілей береді (
, кейде тек қалың әріптермен АВ белгілеу түрлері кездеседі. Сол сияқты векторларды бір әріппен де белгілей береді ( =
=  ,
,  , а).
, а).  векторының ұзындығы деп АВ кесіндісінің ұзындығын айтады және
векторының ұзындығы деп АВ кесіндісінің ұзындығын айтады және  деп белгілейді. Басы мен соңы беттесетін вектор нолдік вектор деп аталады,
деп белгілейді. Басы мен соңы беттесетін вектор нолдік вектор деп аталады,  =
=  және ұзындығы нолге тең.Бір түзудің не өзара параллель түзулер бойында орналасқан векторлар коллениар векторлар деп аталады.
және ұзындығы нолге тең.Бір түзудің не өзара параллель түзулер бойында орналасқан векторлар коллениар векторлар деп аталады.  және
және  векторларының қосындысы «үшбұрыш» не «параллелограмм» ережесімен анықталады:
векторларының қосындысы «үшбұрыш» не «параллелограмм» ережесімен анықталады:

|
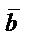
|

|

|

|

|
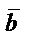
|

|
 және
және  векторларының
векторларының  -
-  айырымы деп
айырымы деп  -ға қосқанда
-ға қосқанда 

|

|

|
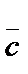 =
=  -
-  векторын айтады.
векторын айтады.
Басы А, соңы В нүктесі болатын бағытталған кесінді вектор деп аталады. Оқулықтарда векторларды  немесе
немесе 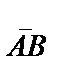 , кейде тек қалың әріптермен АВ белгілеу түрлері кездеседі. Сол сияқты векторларды бір әріппен де белгілей береді (
, кейде тек қалың әріптермен АВ белгілеу түрлері кездеседі. Сол сияқты векторларды бір әріппен де белгілей береді ( =
=  ,
,  , а).
, а).  векторының ұзындығы деп АВ кесіндісінің ұзындығын айтады және
векторының ұзындығы деп АВ кесіндісінің ұзындығын айтады және  деп белгілейді. Басы мен соңы беттесетін вектор нолдік вектор деп аталады,
деп белгілейді. Басы мен соңы беттесетін вектор нолдік вектор деп аталады,  =
=  және ұзындығы нолге тең.Бір түзудің не өзара параллель түзулер бойында орналасқан векторлар коллениар векторлар деп аталады.
және ұзындығы нолге тең.Бір түзудің не өзара параллель түзулер бойында орналасқан векторлар коллениар векторлар деп аталады.  және
және  векторларының қосындысы «үшбұрыш» не «параллелограмм» ережесімен анықталады:
векторларының қосындысы «үшбұрыш» не «параллелограмм» ережесімен анықталады:

|
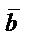
|

|

|

|

|
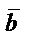
|

|
 және
және  векторларының
векторларының  -
-  айырымы деп
айырымы деп  -ға қосқанда
-ға қосқанда 

|

|

|
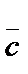 =
=  -
-  векторын айтады.
векторын айтады.
 векторының
векторының 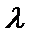 санға көбейтіндісі деп ұзындығы
санға көбейтіндісі деп ұзындығы  болатын, бағыты
болатын, бағыты 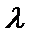 >0 болғанда
>0 болғанда  векторымен бағыттас,
векторымен бағыттас, 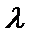 <0 болғанда
<0 болғанда  векторымен қарама-қарсы бағытта болатын
векторымен қарама-қарсы бағытта болатын  векторын айтады. Суретте,
векторын айтады. Суретте, 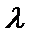 = 2,
= 2,  =2
=2  ;
; 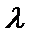 = -1,
= -1,  =-
=-  .
.
Не нашли, что искали? Воспользуйтесь поиском: