Элементы теории множеств и математической логики. Действительные числа. Грани. Понятие функции. Обратная функция.

Числовые множества задаются на оси действительных чисел R. На этой оси выбирают масштаб и указывают начало отсчета и направление. Наиболее распространенные числовые множества:

‑ множество натуральных чисел;

‑ множество целых чисел;

– множество рациональных или дробных чисел;

‑ множество действительных чисел.

Кантор описывает множество следующим образом:

Множество есть любое собрание определенных и различимых между собой объектов нашей интуиции и интеллекта, мыслимое как единое целое. Эти объекты называются элементами множества .

Грани. Множество всех рациональных чисел является счетным множеством. Счетным является множество всех точек плоскости (пространства) имеющих рациональные координаты.

Множество всех действительных чисел является несчетным: оно имеет мощность, называемую континуумом.

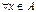Некоторое непустое подмножество множества действительных чисел называют ограниченным сверху (снизу), если существует действительное число такое, что выполняется неравенство ().

Всякое число с указанным свойством называют верхней (нижней) гранью множества .

Непустое подмножество множества действительных чисел называется ограниченным, если оно ограничено и сверху и снизу.

В противоположность этому определению, множество называется неограниченным сверху (снизу), если какое бы число мы бы не предложили в качестве верхней (нижней) границы множества , всегда найдется элемент этого множества, который будет больше (меньше) .

Множество, неограниченное как сверху, так и снизу, называется неограниченным множеством.

Наименьшую из верхних граней непустого подмножества множества действительных чисел называют точной верхней гранью этого множества и обозначают sup . Наибольшую из нижних граней непустого подмножества множества действительных чисел называют точной нижней гранью этого множества и обозначают inf . Символы sup и inf являются сокращениями от supremum (самый верхний) и infimum (самый нижний).

Примем без доказательства утверждение о том, что всякое ограниченное сверху (снизу) множество имеет точную верхнюю (нижнюю) грань.

Обра́тная фу́нкция — функция, обращающая зависимость, выражаемую данной функцией.

16.Понятие последовательности и ее предела. Бесконечно малые. Свойства пределов. Монотонные последовательности. Число «е».

Числовой последовательностью называется числовая функция, определенная на множестве натуральных чисел.

Если функцию задать на множестве натуральных чисел , то множество значений функции будет счетным и каждому номеру ставится в соответствие число . В этом случае говорят, что задана числовая последовательность. Числа называют элементами или членами последовательности, а число – общим или –м членом последовательности. Каждый элемент имеет последующий элемент . Это объясняет употребление термина «последовательность».

Задают последовательность обычно либо перечислением ее элементов , либо указанием закона, по которому вычисляется элемент с номером , т.е. указанием формулы ее ‑го члена .

Бесконечный предел

Наряду с бесконечно малыми существуют и бесконечно большие величины, являющиеся обратными по отношению к бесконечно малым. Поэтому является бесконечно большой (, при ), если такое, что при .

Говорят, что предел последовательности равен , если для такое, что выполняется неравенство: .

В отличие от бесконечно малых последовательностей, бесконечно большие могут не иметь предела. Например, по модулю неограниченно растет, но сама величина не имеет определенного стремления.

Свойства пределов:

Пределы обладают следующими свойствами:

· Если – есть постоянная функция, то ;

· Если существуют , и в некоторой окрестности точки функция 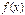ограничена, т.е. , тогда ;

· Если существуют и при каком-то условии, то (при том же условии). Это свойство справедливо для любого конечного числа функций;

· Если существуют и при каком-то условии, то 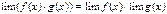(при том же условии). Это свойство также справедливо для любого конечного числа функций, в частности, справедлива формула ;

· Если существуют и при каком-то условии, то (при том же условии);

· Если и существуют , и , то .

Монотонная последовательность — это последовательность, элементы которой с увеличением номера не убывают, или, наоборот, не возрастают. Подобные последовательности часто встречаются при исследованиях и имеют ряд отличительных особенностей и дополнительных свойств. Последовательность из одного числа не может считаться возрастающей или убывающей.

Число «e» — математическая константа, основание натурального логарифма, трансцендентное число. Иногда число e называют числом Эйлера или числом Непера. Обозначается строчной латинской буквой «e».Число e играет важную роль в дифференциальном и интегральном исчислении, а также во многих других разделах математики.

Не нашли, что искали? Воспользуйтесь поиском: