
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Квадратичные формы, приведение их к каноническому виду. Знакоопределенность форм. Критерий Сильвестра.
Понятие квадратичной формы
Первоначально теория квадратичных форм использовалась для исследования кривых и поверхностей, задаваемых уравнением второго порядка, содержащими две или три переменные, Позднее эта теория нашла и другие приложения. В частности, при математическом моделировании экономических процессов целевые функции могут содержать квадратичные слагаемые. Многочисленные приложения квадратичных форм потребовали построения общей теории, когда число переменных равно любому  , а коэффициенты квадратичной формы не всегда являются вещественными числами.
, а коэффициенты квадратичной формы не всегда являются вещественными числами.
Квадратичной формой  от
от  неизвестных
неизвестных  называется сумма, каждое слагаемое которой является либо квадратом одного из неизвестных, либо произведением двух разных неизвестных.
называется сумма, каждое слагаемое которой является либо квадратом одного из неизвестных, либо произведением двух разных неизвестных.
Канонический базис квадратичной формы
Принято считать, что квадратичная форма  имеет канонический вид, если все коэффициенты при произведениях различных переменных равны нулю, т.е.
имеет канонический вид, если все коэффициенты при произведениях различных переменных равны нулю, т.е.  при
при  . При этом квадратичная форма представляет собой сумму квадратов переменных с соответствующими коэффициентами
. При этом квадратичная форма представляет собой сумму квадратов переменных с соответствующими коэффициентами  , т.е.:
, т.е.:
 .
.
В этом случае матрица квадратичной формы имеет диагональный вид:

Очевидно, что изучение свойств квадратичной формы, записанной в каноническом виде, значительно упрощается. В связи с этим возникает задача приведения произвольной квадратичной формы к каноническому виду. В основе многих известных методов приведения квадратичной формы к каноническому виду лежит следующая теорема.
Теорема. Всякая квадратичная форма с помощью невырожденного линейного преобразования может быть приведена к каноническому виду.
Теорема (Критерий Сильвестра). Справедливы следующие утверждения:
1. Квадратичная форма  положительно определена тогда и только тогда, когда главные миноры матрицы
положительно определена тогда и только тогда, когда главные миноры матрицы  положительны.
положительны.
2. Квадратичная форма 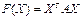 отрицательно определена тогда и только тогда, когда главные миноры матрицы
отрицательно определена тогда и только тогда, когда главные миноры матрицы  четного порядка положительны, а главные миноры матрицы
четного порядка положительны, а главные миноры матрицы  нечетного порядка отрицательны.
нечетного порядка отрицательны.
Доказательство: Докажем первое утверждение.
Необходимость. Дано, что  положительно определена. Покажем, что все угловые миноры матрицы
положительно определена. Покажем, что все угловые миноры матрицы  отличны от нуля. Допустим обратное, и пусть
отличны от нуля. Допустим обратное, и пусть  . Тогда согласно Лемме найдется такой ненулевой вектор
. Тогда согласно Лемме найдется такой ненулевой вектор 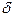 , что
, что  . Однако это противоречит положительной определенности квадратичной формы.
. Однако это противоречит положительной определенности квадратичной формы.
Итак, матрица  удовлетворяет условию Якоби, поэтому можно построить систему векторов Якоби
удовлетворяет условию Якоби, поэтому можно построить систему векторов Якоби 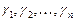 , которая является каноническим базисом
, которая является каноническим базисом 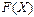 , причем выражение
, причем выражение  – ее канонический вид в базисе
– ее канонический вид в базисе 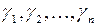 . Теперь из положительной определенности квадратичной формы и первого утверждения доказанной ранее теоремы следует, что
. Теперь из положительной определенности квадратичной формы и первого утверждения доказанной ранее теоремы следует, что  , и значит, что
, и значит, что  .
.
Достаточность. Если  , то угловые миноры матрицы
, то угловые миноры матрицы  отличны от нуля, и можно построить канонический базис квадратичной формы
отличны от нуля, и можно построить канонический базис квадратичной формы  , в котором
, в котором  – канонический вид квадратичной формы
– канонический вид квадратичной формы 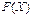 . Поскольку
. Поскольку  , то
, то  положительно определена.
положительно определена.
Аналогично доказывается второе утверждение теоремы.
14.Поверхности второго порядка, их классификация. Поверхность второго порядка — геометрическое место точек трёхмерного пространства, прямоугольные координаты которых удовлетворяют уравнению вида

в котором по крайней мере один из коэффициентов  ,
,  ,
,  ,
,  ,
,  ,
,  отличен от нуля.
отличен от нуля.
Классификация поверхностей второго порядка:
- эллипсоид, -мнимый эллипсоид, -мнимый конус, -однополюсный эллипсоид, - двухполюсный эллипсоид,
-конус, -эллиптический параболоид, -гиперболический параболоид, -эллиптический цилиндр,
-мнимый эллиптический цилиндр, -гиперболический цилиндр,-параболоидный цилиндр.
Не нашли, что искали? Воспользуйтесь поиском: