
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Свойства комплексных чисел. Разложение многочленов на множители. Представление рациональной функции в виде суммы элементарных дробей.
Комплексные числа — числа вида  , где
, где 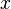 и
и  — вещественные числа,
— вещественные числа,  — мнимая единица; то есть
— мнимая единица; то есть  . Множество всех комплексных чисел обычно обозначается
. Множество всех комплексных чисел обычно обозначается 
Первоначально идея о необходимости расширения понятия действительного числа возникла в результате формального решения квадратных и кубических уравнений, в которых в формулах для корней уравнения под знаком корня стояло отрицательное число. В дальнейшем возникшая теория функций комплексного переменного нашла применение для решения многих задач во всех областях математики и физики.
Тождественное преобразование, приводящее к произведению нескольких множителей - многочленов или одночленов, называют разложением многочлена на множители. В этом случае говорят, что многочлен делится на каждый из этих множителей.
-Вынесение общего множителя за скобки. Это преобразование является непосредственным следствием распределительного закона ac + bc = c(a + b).
-Использование формул сокращенного умножения. Формулы сокращённого умножения позволяют довольно эффективно представлять многочлен в форме произведения.
-Способ группировки. Этот способ заключается в том, что слагаемые многочлена можно сгруппировать различными способами на основе сочетательного и переместительного законов. На практике он применяется в тех случаях, когда многочлен удается представить в виде пар слагаемых таким образом, чтобы из каждой пары можно было выделить один и тот же множитель. Этот общий множитель можно вынести за скобку и исходный многочлен окажется представленным в виде произведени.
-Способ выделения полного квадрата. Метод выделения полного квадрата является одним из наиболее эффективных методов разложения на множители. Суть его состоит в выделении полного квадрата и последующего применения формулы разности квадратов.
Для интегрирования рациональной функции  , где P (x) и Q (x) - полиномы, используется следующая последовательность шагов:
, где P (x) и Q (x) - полиномы, используется следующая последовательность шагов:
1. Если дробь неправильная (т.е. степень P (x) больше степени Q (x)), преобразовать ее в правильную, выделив целое выражение;
2. Разложить знаменатель Q (x) на произведение одночленов и/или несократимых квадратичных выражений;
3. Разложить рациональную дробь на простейшие дроби, используя метод неопределенных коэффициентов;
Не нашли, что искали? Воспользуйтесь поиском: