Понятие определенного интеграла и его свойства. Интегрирование кусочно-непрерывных функций. Замена переменной и интегрирование по частям. Формула Ньютона-Лейбница.

Основные свойства определенного интеграла

1. Будем считать, что определенный интеграл с одинаковыми пределами интегрирования равен нулю (по определению):

.

2. Будем считать, что при перемене мест верхнего и нижнего пределов интегрирования определенный интеграл меняет знак на противоположный:

.

3. Пусть функции и интегрируемы на сегменте , тогда функции , и также интегрируемы на этом сегменте, причем:

.

4. Если функция интегрируема на сегменте , то функция ( =const) интегрируема на этом сегменте, причем:

.

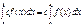5. Если функция интегрируема на сегменте , то эта функция интегрируема на любом сегменте , содержащемся в сегменте .

6. Пусть функция интегрируема на сегментах и . Тогда эта функция интегрируема на сегменте , причем:

.

Основные правила интегрирования

Теорема: Любая непрерывная на интервале функция 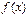имеет на этом интервале первообразную. Одной из первообразных является функция:

,

где - любая фиксированная точка интервала .

Так как две первообразные данной функции отличаются на постоянную, то согласно теореме, любая первообразная непрерывной на сегменте функции имеет вид:

где - некоторая постоянная.

Полагая в последней формуле сначала 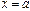, затем , и используя первое свойства определенного интеграла, получим:

, .

Из этих равенств вытекает соотношение:

,

которое называется основной формулой интегрального исчисления или формулой Ньютона – Лейбница.

Пусть выполнены следующие условия:

1) Функция непрерывна на отрезке ;

2) отрезок является множеством значений некоторой функции , определенной на отрезке и имеющей на этом отрезке непрерывную производную;

3) , .

При этих условиях справедлива формула:

Указанная формула называется формулой замены переменной в определенном интеграле.

Пусть функции и имеют непрерывные производные на сегменте . Тогда имеет место следующая формула интегрирования по частям для определенных интегралов:

.

Так как и , то эту формулу можно записать следующим образом:

.

28.Геометрические приложения определенного интеграла. Физические приложения. 1. Площадь криволинейной трапеции, ограниченной кривой y =f(x)(f(x)>0), прямыми x = a, x = b и отрезком [ a, b ] оси Ох, вычисляется по формуле

2. Площадь фигуры, ограниченной кривыми y = f (x) и y = g (x) (f (x)< g (x)) и прямыми х= a, x = b, находится по формуле

3. Если кривая задана параметрическими уравнениями x = x (t), y = y (t), то площадь криволинейной трапеции, ограниченной этой кривой и прямыми х=a, x= b, находится по формуле

4. Пусть S (x)- площадь сечения тела плоскостью, перпендикулярной оси Ох, тогда объем части тела, заключенной между перпендикулярными оси плоскостями х=а и х= b, находится по формуле

5. Пусть криволинейная трапеция, ограниченная кривой y = f (x) и прямыми y=0, х=а и х= b, вращается вокруг оси Ох, тогда объем тела вращения вычисляется по формуле

6. Пусть криволинейная трапеция, ограниченная кривой х= g (y) и

прямыми x =0, y = c и y = d, вращается вокруг оси О y, тогда объем тела вращения вычисляется по формуле

7. Если плоская кривая отнесена к прямоугольной системе координат и задана уравнением y = f (x) (или x = F (y)), то длина дуги определяется формулой

Не нашли, что искали? Воспользуйтесь поиском: