
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Исследование функции на экстремум, монотонность и точки перегиба функции.
Монотонность функции
Функция  называется возрастающей на промежутке
называется возрастающей на промежутке  , если
, если  для любых точек
для любых точек  и
и 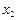 из промежутка
из промежутка  , удовлетворяющих неравенству
, удовлетворяющих неравенству  . Функция называется убывающей на
. Функция называется убывающей на 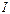 , если из условия
, если из условия  следует
следует  .
.
Теорема. Если функция  непрерывна на отрезке
непрерывна на отрезке  , дифференцируема на интервале
, дифференцируема на интервале 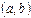 , то для того, чтобы
, то для того, чтобы  была возрастающей (убывающей) необходимо и достаточно, чтобы
была возрастающей (убывающей) необходимо и достаточно, чтобы 
 в каждой внутренней точке интервала
в каждой внутренней точке интервала  .
.
Дифференцируемая функция является возрастающей на промежутке  тогда и только тогда, когда
тогда и только тогда, когда  .
.
Выпуклость и перегибы графика функции
Графиком функции  , заданной на множестве
, заданной на множестве  , называют множество точек плоскости с координатами
, называют множество точек плоскости с координатами  . График называют выпуклым вниз на промежутке
. График называют выпуклым вниз на промежутке  , если касательная к графику в любой точке этого промежутка расположена ниже графика. Если касательная расположена выше графика, то график называют выпуклым вверх. Точка, в которой график меняет направление выпуклости, называется точкой перегиба.
, если касательная к графику в любой точке этого промежутка расположена ниже графика. Если касательная расположена выше графика, то график называют выпуклым вверх. Точка, в которой график меняет направление выпуклости, называется точкой перегиба.
Если на промежутке  вторая производная
вторая производная 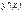 положительна, то график является выпуклым вниз на этом промежутке. Если
положительна, то график является выпуклым вниз на этом промежутке. Если  на промежутке
на промежутке  , то график является выпуклым вверх на промежутке
, то график является выпуклым вверх на промежутке  .
.
Точка  может быть точкой перегиба только в том случае, когда
может быть точкой перегиба только в том случае, когда 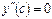 , либо
, либо  не существует – необходимое условие перегиба. Однако равенство нулю или не существование второй производной в точке
не существует – необходимое условие перегиба. Однако равенство нулю или не существование второй производной в точке  не означает еще, что в точке
не означает еще, что в точке  будет перегиб графика. Поэтому нужно дополнительно исследовать такие точки.
будет перегиб графика. Поэтому нужно дополнительно исследовать такие точки.
I правило. Если  равна нулю или не существует и
равна нулю или не существует и  при переводе через точку
при переводе через точку  меняет знак, то
меняет знак, то  ‑ точка перегиба графика функции
‑ точка перегиба графика функции  .
.
II правило. Если  и
и 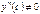 , то
, то  является точкой перегиба графика функции
является точкой перегиба графика функции  .
.
Локальный экстремум
Точка  называется точкой локального максимума функции
называется точкой локального максимума функции  , если существует интервал
, если существует интервал  , содержащий точку
, содержащий точку  такой что
такой что  .
.
Точка  называется точкой локального минимума функции
называется точкой локального минимума функции  , если существует интервал
, если существует интервал  , содержащий точку
, содержащий точку  такой что
такой что  .
.
Точки локального минимума и локального максимума называются точками локального экстремума.
Необходимым условием локального экстремума дифференцируемой функции является выполнение равенства  . Поэтому точки, в которых дифференцируемая функция может иметь локальный экстремум, находят, решая уравнение:
. Поэтому точки, в которых дифференцируемая функция может иметь локальный экстремум, находят, решая уравнение:  .
.
Решения этого уравнения называют стационарными точками.
Глобальный экстремум
Непрерывная на отрезке  функция
функция  принимает свое наибольшее значение
принимает свое наибольшее значение  и свое наименьшее значение
и свое наименьшее значение  в точках этого отрезка. Эти значения могут достигаться либо в стационарных точках отрезка, либо в точках недифференцируемости функции, либо в граничных точках отрезка. Поэтому для нахождения значений
в точках этого отрезка. Эти значения могут достигаться либо в стационарных точках отрезка, либо в точках недифференцируемости функции, либо в граничных точках отрезка. Поэтому для нахождения значений  и
и  поступают следующим образом.
поступают следующим образом.
· Находят стационарные точки 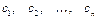 функции;
функции;
· Находят точки  , в которых производная
, в которых производная  не существует или обращается в бесконечность;
не существует или обращается в бесконечность;
· Вычисляют значения:
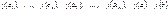 ‑ и выбирают среди этих чисел наибольшее и наименьшее.
‑ и выбирают среди этих чисел наибольшее и наименьшее.
Это и будут  и
и  ‑ глобальные экстремальные значения.
‑ глобальные экстремальные значения.
Не нашли, что искали? Воспользуйтесь поиском: