Вычислить интегралы от простейших дробей.

Первообразная. Неопределенный интеграл и его свойства. Таблица интегралов. Основные методы вычисления.

Понятие неопределенного интеграла

Интегрирование – операция, обратная дифференцированию, которая позволяет определять функцию , для которой заданная функция является ее производной:

.

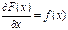Другими словами, если операция дифференцирования состоит в нахождении производной, то интегрирование – это операция отыскания первообразной.

Функция называется первообразной для функции , на промежутке , если для каждой точки этого промежутка .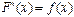

Теорема. Если и – любые две первообразные для данной функции на промежутке , то для всех выполняется равенство .

Доказательство:

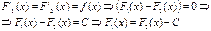
Таким образом, все семейство первообразных для данной функции имеет вид , где одна из первообразных, а 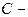произвольная постоянная.

Совокупность всех первообразных для функции на промежутке называется неопределенным интегралом функции .

Неопределенный интеграл обозначается следующим образом:

,

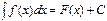где знак интеграла;

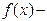подынтегральная функция;

подынтегральное выражение.

Свойства неопределенного интеграла

1.Производная неопределенного интеграла равна подынтегральной функцией:

2.

Эти свойства означают, что интегрирование и дифференцирование – взаимно обратные операции.

3.Если 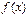и – интегрируемые функции, т.е. на промежутке они имеют первообразные, то сумма функций также интегрируема и .

4.Если 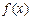– интегрируемая функция, а 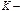постоянная величина, то – также интегрируемая функция и .

Таким образом, свойства 3 и 4 указывают на линейность операции интегрирования:

,

где постоянные;

интегрируемые функции.

5.Если , а также дифференцируемая функция, то .

Простым обращением известных формул дифференцирования элементарных функций получается таблица простейших неопределенных интегралов.

1. ;

2. ;

3. ;

4. ;

5. ;

6. ;

7. ;

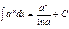
8. ;

9. ;

10. ;

Не нашли, что искали? Воспользуйтесь поиском: