Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.

Линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами называется уравнение

y'' + py' +qy = 0

где p и q – числа.

Для того, чтобы решить это уравнение надо составить характеристическое уравнение, которое получается из данного уравнения, если в нем заменить y"=k², y'=k, a y=k⁰=1.

k² + pk + q = 0 -

- это квадратное уравнение.

Общее решение характеристического уравнения строиться в зависимости от характера его корней.

Возможны три случая:

- дискриминант квадратного уравнения больше нуля D > 0, уравнение имеет два действительный различных корня, k₁≠ k₂, и общее решение характеристического уравнения имеет вид:

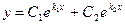
- дискриминант характеристического квадратного уравнения равен нулю D= 0, уравнение имеет два действительный кратных корня, k₁= k₂= k, и общее решение уравнения имеет вид:

- дискриминант квадратного уравнения меньше нуля D < 0, уравнение имеет пару комплексно сопряженных корней, k_1,2= α ± βi, и общее решение уравнения имеет вид:

Пример 10.8. Найти общее решение дифференциального уравнения

y"+7y'+6y=0.

Решение. Составим характеристическое уравнение

k²+7k+6=0.

Решим его: D=49-24=25, k₁= -1, k₂ = -6. Так как корни действительные и разные, то, согласно формулы, получаем общее решение:

y = C₁e^-x + C₂e^-6x.

Пример 10.9. Найти общее решение дифференциального уравнения

y"-6y'+9y=0.

Решение. Составим характеристическое уравнение

k² - 6k +9=0.

Решим это уравнение: D = 36 -36 = 0, k₁ = k₂ =3. Характеристическое уравнение имеет два действительных кратных корня, следовательно, общее решение находим по формуле:

y = (C₁x + C₂)e^3x.

Пример 10.10. Найти общее решение дифференциального уравнения

y"-4y'+13y=0.

Решение. Составим характеристическое уравнение

k² – 4k +13 = 0.

Решим его. Дискриминант квадратного уравнения меньше нуля, D=-36, уравнение имеет пару комплексно сопряженных корней, k_1,2=

(α=2, β=3) и общее решение уравнения имеет вид:

y = e^2x(C₁cos3x + C₂sin3x).

Пример 10.11. Найти частное решение дифференциального уравнения

y"-5y'+4y=0, удовлетворяющее начальным условиям у'(0)=8, у(0)=5.

Решение. Сначала найдем общее решение, для этого составим

характеристическое уравнение

k² – 5k +4 = 0.

Дискриминант этого уравнения D=1, следовательно, уравнение имеет два действительный корня, k₁ = 2, k₂ = 3 и общее решение уравнения имеет вид:

y = С₁e^2x +C₂e^3x.

Чтобы найти частное решение, сначала найдем у'=2С₁e^2x +3C₂e^3x, а затем подставим в общее решение и в производную от функции-решения у начальные условия и получим систему для определения постоянных С₁ и С₂.

.

Решив систему получили С₁=7, С₂ = -2.

Таким образом искомое частное решение имеет вид: y =7e^2x – 2e^3x.

Не нашли, что искали? Воспользуйтесь поиском: