Однородные уравнения.

Уравнения вида 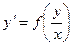называется однородным дифференциальным уравнением первого порядка.

Однородное уравнение приводиться к уравнению с разделяющимися переменными подстановкой y=u∙x, где u=u(x) - новая искомая функция. Заменим у и y'= u'x + u в данном уравнении:

u'x + u = f(u)

Разделив переменные, получаем:

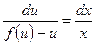
Проинтегрировав, полученное уравнение найдем общее решение или общий интеграл.

Пример 10.3. Найти общее решение дифференциального уравнения

.

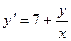Решение. Введем новую функцию 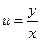, тогда и . Заменяя в исходном уравнении функцию у и ее производную у' получим уравнение с разделяющимися переменными:

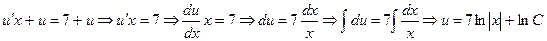
u = lnCx⁷.

Возвращаемся к старой функции .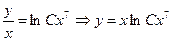

Не нашли, что искали? Воспользуйтесь поиском: