Решение типового примера. Пример 9.4. Исследовать на экстремум функцию .

Пример 9.4. Исследовать на экстремум функцию .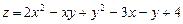

Решение. В соответствие с достаточным условием экстремума функции двух переменных, найдем точки, удовлетворяющие условию:

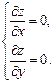
Для этого находим частные производные функции:

; ,

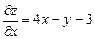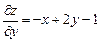затем приравниваем их к нулю и решаем систему уравнений:

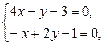
откуда находим 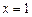, 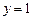. Таким образом, получили точку 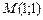, в которой будем продолжать исследовать функцию на экстремум.

Находим значения частных производных второго порядка в точке :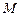

; ; .

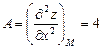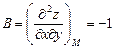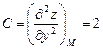Найдем знак дискриминанта 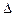в указанной точке:

.

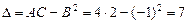Так как дискриминант больше нуля 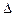> 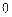и 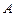> 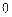, то функция имеет минимум в точке :

.

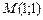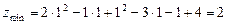Ответ. В точке 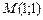функция 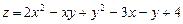имеет минимум .

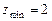Не нашли, что искали? Воспользуйтесь поиском: