Уравнения с разделяющимися переменными.

В общем случае дифференциальные уравнения первого порядка с разделяющимися переменными имеют вид:

P₁(x)Q₁(y)dу + P₂(x)Q₂(y)dх=0

Видно, что в этом уравнении множители перед dx и dy представляют собой произведения двух функций. Одна из которых зависит только от х, а другая - только от у. Следовательно, данное уравнение можно проинтегрировать, предварительно разделив переменные: в одной части уравнения оставить функцию, зависящую только от х, а в другой – только от у, для этого перенесем одно из слагаемых в правую часть и разделим обе части полученного равенства на произведение функций Q₂(y) P₁(x).

Проинтегрировав обе части уравнения, получим:

Пример 10.1. Найти общее решение дифференциального уравнения

xydx+(x+1)dy=0.

Решение. Разделим переменные в данном уравнении, перенеся первое слагаемое в правую часть, и разделив обе части уравнения на выражение у(х+1).

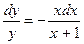
Проинтегрируем обе части полученного равенства:

Найдем общее решение .

Пример 10.2. Найти частное решение дифференциального уравнения

(4+x²)lny∙y' - y = 0,

при следующих начальных условиях y(2)=1.

Решение. Заменив y′ на , и разделив переменные получаем:

.

Получили общий интеграл дифференциального уравнения. Чтобы найти частное решение, можно, сначала, найти частный интеграл. Для этого, в общий интеграл подставим начальные условия x=2 и y=1 и находим С.

Окончательно получаем частный интеграл и частное решение:

.

Не нашли, что искали? Воспользуйтесь поиском: