
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Производные функций, заданных параметрическими уравнениями.
Y ’x=  /x’t
/x’t
43.Дифференциал функции. Применение дифференциала к приближённым вычислениям.
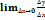 = f(x)(1).
= f(x)(1).
Тогда из (1) имеем:  (2).
(2).
Умножив обе части на 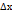 получим:
получим:  (3).
(3).
Дифференциал функции y=f(x) в точке Х наз. главной линейной частью f’(x) *  x________________dy=f(x)*
x________________dy=f(x)*  x (4).
x (4).
Если формулу (4) применить к самому аргументу Х, т.е. к функции y=f(x)=x, то учитывается что х'=1 получим: dx=  x (5). Учитывая равенство (5), формулу (4) можно записать в виде: dy=f’(x) * dx (6).
x (5). Учитывая равенство (5), формулу (4) можно записать в виде: dy=f’(x) * dx (6).
Из формулы (3) следует, что если f’(x)  0, то при
0, то при 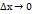 в фиксированной точке х=х 0 будет выполняться:
в фиксированной точке х=х 0 будет выполняться:  или
или 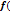 x0 +
x0 +  x) – f (x0)
x) – f (x0) 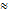 f (x0 -
f (x0 -  ) (7).
) (7).
Правило Лопиталя.
Пусть функция f(x) и g(x) дифференцированны в окрестные точки Х0 и g’(x)  .
.
Если 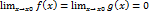
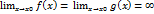 , т.е. частное f(x)/g(x) представляет собой неопределённость вида 0/0 или
, т.е. частное f(x)/g(x) представляет собой неопределённость вида 0/0 или  , то
, то  при условии что существует.
при условии что существует.
Замечание1 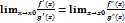
Замечание2 Неопределённость вида  приводится к неопределённому пределу
приводится к неопределённому пределу  , а неопред. вида 0
, а неопред. вида 0 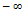 к неопред. виду
к неопред. виду  или
или  путём алгебраических преобразований исследования функции.
путём алгебраических преобразований исследования функции.
Не нашли, что искали? Воспользуйтесь поиском: