Возрастание и убывание функций. Точки экстремума функции.

Определение1 Функция y=f(x) наз. возрастающей в интервале (а,в), если для любого Х_{1 2}, где Х1,Х2 (а,в), выполняется условие f(X1) f(X2).

Определение2 Функция y=f(x) наз. убывающей в интервале (а,в), если для любого Х1 Х2, где Х1,Х2 (а,в) выполняется след. условие f(X1) f(X2).

Возрастание или убывание в некотором интервале (а,в), функция наз. монотонной в этом интервале.

Теорема1 Если ф-ция y=f(x) дифференцирован в интервале (а,в) и f'(x) 0 при всех Х (а,в), то функция f(x) в интервале (а,в), но если f’(x)<0 при всех Х (а,в), то ф-ция f(x) в интервале(а,в).

Определение3 Точка Х₀ наз. min функции y=f(x), если существует такая -окрестность V(X₀,v) точки Х₀ что для любого Х V(X₀,v) выполняется неравенство f(x₀)<f(x). Если же для любого х V(X₀,v) выполняется неравенство f(x₀) > f(x), то точка Х₀ наз. точкой max.

При этом число f(X₀) наз. min(max) функции. Точки min(max) наз. её точками экстремума.

Теорема2 Если функция y = f(x)в точке x₀ имеет экстремуму, то f’(x)=0 или f’(x) не существует.

Теорема3 Пусть функция y = f(x) дифференцирова в некоторой v - окресности V(x₀,v)=(x₀-v, x₀+v) точки X₀ за исключением могут быть самой точки Х_0. Если f’(x)>0 для любого x 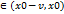и f’(x)<0 для любого х .

Теорема4 Пустьf’(x₀)=0 или f”(x₀) . Тогда функция y = f(x) имеет в точке Х₀ max, если f”(x₀)<0 и min, если f”(x₀)>0.

Не нашли, что искали? Воспользуйтесь поиском: