Система с фиксированным размером заказа

Важнейшими параметрами, необходимыми для работы системы, являются оптимальный размер заказа (q_o) и пороговый уровень запасов (ПУ).

Рассчитаем оптимальный размер заказа листовой стали по формуле (2.8) с учетом исходных данных.

Так как транспортные расходы на выполнение одного заказа (С^e_o), а также затраты на хранение 1т стали (С^e_хр) зависят от размера заказа, который еще предстоит определить, необходимо в качестве первого приближения установить размер заказа.

Принимаем размер заказа 10т, тем самым предполагая, что для транспортировки будет использоваться автотранспорт.

Во-первых, определяем транспортные расходы на выполнение одного заказа (С^е_о) по доставке листовой стали из Москвы. По состоянию на 01.01.2011 г. величина тарифной ставки на оказание автотранспортных услуг для автотранспортного агрегата грузоподъемностью 10т составляла в среднем 1,5тыс.руб. за 1км. Следовательно, издержки на выполнение одного заказа из Москвы (1500км туда и обратно) составят 2250тыс.руб. (1500км·1,5тыс.руб./км).

Во-вторых, определяем издержки на хранение 1т стали в течение года (С^е_хр). С учетом линейных размеров стального листа (6000х1500мм), допустимой нагрузки на 1м² пола для складов по хранению стали (4т/м²), а также ширины проходов и проездов минимальная необходимая площадь хранения должна составлять 15м². Рассчитаем издержки на хранение 1т стали (С^е_хр) за год.

Они составят 252тыс.руб. (15м²·7тыс.руб./(мес.·м²)·12мес.: 5т), где 5т – среднее количество стали (средний остаток), которое будет находиться на складе (q/2 = 10/2).

Принимая значение коэффициента эффективности финансовых вложений (Е) за период времени, равный одному году, на уровне 0,5 (предполагая возможность дальнейшего наращивания производственной программы новых изделий), определяем размер заказа согласно зависимости (2.8):

Полученный расчетный размер заказа (16,8т) позволяет утверждать, что принятый интуитивно размер заказа 10т значительно отличается от оптимальной величины.

В этой связи осуществляем второе приближение. Для этого ус­танавливаем размер заказа с определенным опережением к уровню 16,8т, принимая его равным 20т.

Уточняем транспортные расходы на выполнение одного заказа (С^е_о) по доставке листовой стали из Москвы. По состоянию на 01.01.2011г. величина тарифной ставки на оказание автотранспортных услуг для автотранспортного агрегата грузоподъемностью 20т составляла в среднем 1,9тыс. руб. за 1км. Следовательно, издержки на выполнение одного заказа из Москвы (1500км туда и обратно) будут равны 2850тыс.руб. (1500 км·1,9тыс.руб./км).

Уточняем издержки на хранение 1т стали в течение года (С^е_хр). Они составят 126тыс.руб. (15м²·7тыс.руб./мес.м²)х12мес.:10т), где 10т – среднее количество стали (средний остаток), которое будет находиться на складе (q/2 = 20/2).

Уточняем размер заказа согласно зависимости (2.8):

Принятый размер заказа согласно второму приближению (20т) практически не отличается от оптимальной величины (19,7т), поэтому окончательно устанавливаем размер заказа на уровне 20т.

На рис. 2.8 представлен график, который отражает зависимость издержек, связанных с формированием и управлением запасами листовой стали, от размера заказа с учетом потерь денежных ресурсов, вложенных в создание запасов затрат (С_п), согласно формуле

Рис. 2.8. Зависимость издержек, связанных с формированием и управлением запасами листовой стали,

от размера заказа

Рассчитаем размер заказа листовой стали по формуле Уилсона (2.5) с учетом исходных данных и того, что ее доставка предположительно будет осуществляться автотранспортом:

Полученное значение оптимального размера заказа, согласно формуле Уилсона, позволяет утверждать, что доставка листовой стали должна осуществляться не автомобильным, а железнодорожным транспортом, так как максимальный размер одной партии поставки автомобильным транспортом ограничивается грузоподъемностью автотранспортного агрегата (фуры), которая обычно не превышает 25т.

В свою очередь, минимальная площадь склада, занимаемая сталью, должна составлять не 15м², а не менее 30м². Это объясняется тем что на 9м² площади пола, которую занимает один стальной лист (6000х1500мм) с учетом допустимой нагрузки на 1м² (4т/м²), максимально можно хранить не более 36т стали. Чтобы разместить 67,3т стали с учетом ширины проходов и проездов, потребуется не 15м², а 30м² площади склада.

Уточним оптимальный размер заказа по формуле Уилсона. Во-первых, пересчитаем транспортные расходы на выполнение одного заказа (С^е_о) по доставке листовой стали из Москвы. По состоянию на 01.01.201 г. величина тарифной ставки на оказание услуг железнодорожного транспорта составляла в среднем 6тыс.руб. за 1 вагоно-километр. Следовательно, издержки на выполнение одного заказа из Москвы (750км в одну сторону) с учетом того, что потребуется один вагон, составят 4500тыс.руб. (1 вагон·750км х 6тыс. руб./км·вагон).

Пересчитаем издержки на хранение 1 т стали в течение года (С^е_хр). Они составят 63тыс.руб. (30м²·7тыс.руб./(мес.·м²)·12мес.:40т), где 40т – предполагаемое среднее количество стали, которое будет находиться на складе.

Тогда уточненный размер заказа, согласно формуле Уилсона, составит:

Уточненный, согласно формуле Уилсона, размер заказа позволяет утверждать, что для транспортировки стали потребуется два вагона, а для хранения стали – четыре штабеля. Пересчитаем издержки на транспортировку и хранение.

Издержки на выполнение одного заказа из Москвы (750км в одну сторону) с учетом того, что потребуется два вагона, составят 9000 тыс. руб. (2 вагона·750км·6тыс.руб./км·вагон).

Издержки на хранение 1т стали в течение года (С^е_хр) составят 72тыс.руб. (60м²·7тыс.руб./(мес.·м²)·12мес.:70т), где 70т – предполагаемое среднее количество стали, которое будет находиться на складе.

Тогда уточненный размер заказа, согласно формуле Уилсона, составит:

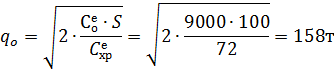
Вновь полученный размер заказа позволяет утверждать, что для хранения стали потребуется пять штабелей. Следовательно, издержки на хранение 1т стали в течение года (С^е_хр) составят 90тыс.руб.(75м²·7тыс.руб./(мес.·м²)·12мес.:70т), где 70т – предполагаемое среднее количество стали, которое будет находиться на складе.

Тогда уточненный размер заказа, согласно формуле Уилсона, составит:

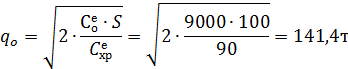
Таким образом, размер заказа, согласно формуле Уилсона, ко­леблется в пределах 150т листовой стали. При этом издержки на хранение 1т стали в течение года (С^е_хр) составят 84тыс.руб.(75м²·7тыс.руб./(мес.·м²)·12мес.:75т).

Анализ полученных результатов показывает, что оптимальный размер заказа, согласно формуле (2.8), в 7,5 раза меньше по сравнению с размером заказа согласно формуле Уилсона.

Определим размер годового экономического эффекта по зави­симости

где С_с1 – совокупные годовые издержки на формирование и управление запасами при размере заказа, рассчитанном согласно формуле Уилсона (2.5), тыс.руб.; С_с2 – совокупные годовые издержки на формирование и управление запасами при размере заказа, рассчитанном согласно формуле (2.8), тыс.руб.

Определим совокупные годовые издержки на формирование и управление запасами с учетом потерь, обусловленных «заморажи­ванием» финансовых средств, которые вложены в создание запасов, при размере заказа, рассчитанном согласно формуле Уилсона:

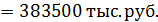
Определим совокупные годовые издержки на формирование и управление запасами при размере заказа, рассчитанном согласно формуле (2.8):

Тогда величина годового экономического эффекта при форми­ровании и управлении запасами при размере заказа, рассчитанном согласно формуле (2.8), составит:

Следовательно, формирование материальных запасов путем осуществления заказов по отдельным наименованиям товаров в размерах, рассчитанных согласно зависимости (2.8), в отличие от формулы Уилсона, позволит получить значительный экономический эффект в результате ускорения оборачиваемости финансового капитала, вкладываемого в создание запасов, а также сокращения издержек, связанных с хранением товаров.

Однако при небольших расстояниях транспортировки (доставки) товара и относительно высоких издержках на хранение единицы товара (С^е_хр) размер заказа, рассчитанный по формуле (2.8), может иметь незначительную величину. В подобных ситуациях размер заказа следует увеличить с учетом ожидаемого потребления товара за время выполнения заказа.

Таким образом, оптимальный (фиксированный) размер заказа (q_o) составляет 20т, или 29 листов (с учетом того, что масса 1 листа равна 0,702т).

Дневное потребление листовой стали на складе определяем как отношение объема ее оборота за год к количеству рабочих дней в году. Его величина будет равна 0,380т(100т:264 рабочих дня).

Пороговый уровень запасов (ПУ) листовой стали представляет собой произведение дневного потребления стали и суммы времени выполнения заказа и задержки поставки. Среднее дневное потребление за рабочий день составляет 380 кг. Согласно исходной информации время выполнения заказа (t_вз) и задержки (t_зп) составляет соответственно 30 и 7 календарных дней или 22 и 6 рабочих дней. Следовательно, пороговый уровень листовой стали составит 10,64т (380кг·(22 + 6)), или 15 листов.

Сравнивая размер заказа (29 листов) и пороговый уровень (15 листов), можно утверждать, что система будет работать.

Гарантийный запас (ГЗ) листовой стали рассчитывается как произведение среднего дневного потребления стали на время задержки поставки и составит 2,28т(380кг·6дн.), или 3 листа.

Максимальный желательный запас (МЖЗ) листовой стали определяется как сумма гарантийного запаса и оптимального размера заказа и составит 22,28т(2,28+20т), или 32 листа. Этот показатель в системе с фиксированным размером заказа используется лишь для того, чтобы определить, сколько места на складе следует выделить для хранения листовой стали, если она хранится в штабеле. Принимая во внимание, что на 9м² площади пола, которую занимает один стальной лист (6000x1500мм), с учетом допустимой нагрузки на 1м² (4т/м²) максимально можно хранить не более 36т стали, утверждаем, что для хранения стали потребуется один штабель, который с учетом проходов и проездов на складе будет занимать не более 15м².

На рис. 2.9 представлен график движения запасов листовой стали за период январь-июнь в соответствии с планируемым потреблением стали (см.табл. 2.1) и расчетными параметрами. При этом было принято, что в нулевой момент времени уровень запасов стали на складе составлял максимальный желательный запас (22,28т).

Анализ графика показывает, что в марте образуется дефицит стали на недельный период (t _д =6 дней) в размере 4т. Это обусловит значительные потери производства, связанные с простоем рабочих мест. Данное обстоятельство вызвано неравномерностью потребления стали в течение года, а также тем, что пороговый уровень запасов рассчитывался, исходя из средней величины потребления (380кг за день), а в марте дневное потребление составит около 680кг.

Рис. 2.9. График движения запасов листовой стали в системе с фиксированным размером заказа (вариант №1)

Решить эту проблему можно в результате пересчета порогового уровня запасов (ПУ), исходя не из среднего, а из максимального месячного потребления стали.

Так, в нашем примере максимальное месячное потребление со­ставляет 15т, или 680кг за рабочий день. Следовательно, пороговый уровень листовой стали составит 19,1т(680кг·(22+6)), или 27 листов. График движения запасов представлен на рис. 2.10.

Анализ рис. 2.10 показывает, что при установлении порогового уровня запасов стали из расчета ее максимального дневного потребления будет наблюдаться бездефицитная работа производства. Однако при этом окажется превышен максимальный желательный уровень запасов. Так, максимальная величина превышения составит порядка 13т (по сравнению с вариантом №1), или на 60%. Между тем это не вызовет увеличения площади склада, занятой листовой сталью (35<36т), где 36т – допустимая нагрузка на 9м². Прямые потери за месяц, связанные с общим увеличением уровня запасов стали («замораживание» финансового капитала), составят порядка 1млн.руб.:

(0,5·9·2,7):12мес. ≈ 1млн.руб.,

где 0,5 – коэффициент эффективности (Е) за период времени, равный одному году; 9 – среднее увеличение уровня запасов на складе для варианта №2 по сравнению с вариантом №1, т; 2,7 – цена 1т стали, млн.руб.

Кроме того, увеличение уровня запасов обусловит выполнение дополнительного заказа стали. Однако связанные с этим издержки носят разовый характер и распространяются на весь период работы производства. Поэтому ими можно пренебречь.

Следовательно, общие потери производства, связанные с управ­лением запасами стали по варианту №2, не превысят 12млн.руб. за год. В свою очередь, управление запасами по варианту №1 вызовет гораздо большие потери, связанные с простоем производства. Так, например, при стоимости производства 1млрд. руб. дневной простой рабочих мест обусловит прямые потери 3-5млн. руб., что более чем в 3 раза превысит потери по варианту №2.

Таким образом, несмотря на увеличение общего уровня запасов стали при управлении ими согласно системе с фиксированным размером заказа по варианту №2, этот вариант является более предпочтительным с экономической точки зрения.

Рис. 2.10. График движения запасов листовой стали в системе с фиксированным размером заказа (вариант №2)

Система с фиксированным интервалом времени между заказами

Важнейшими параметрами, необходимыми для работы системы, являются фиксированный интервал времени между заказами (I) и максимальный желательный уровень запасов (МЖЗ).

Рассчитаем фиксированный интервал времени между заказами по формуле (2.9):

где 264 – количество рабочих дней в году.

Как показывает практика, для простоты применения рассматри­ваемой системы фиксированный интервал времени между заказами рекомендуется измерять не в рабочих, а в календарных днях. В нашем случае его размер составит 74 календарных дня (7·53/5). При этом следует подчеркнуть, что в случае, если имеет место 7-дневная рабочая неделя, количество календарных дней будет равно количеству рабочих дней.

Гарантийный запас (ГЗ) листовой стали рассчитывается как произведение среднего дневного потребления стали на время задержки поставки (рабочих дней) и составит 2,28т(380кг·6дн).

Максимальный желательный запас (МЖЗ) листовой стали определяется как сумма гарантийного запаса и произведения среднего дневного потребления стали на фиксированный интервал времени между заказами и составит 22,3т(2,28+0,38·53).

Для системы управления запасами с фиксированным интервалом времени между заказами важно определить момент времени первого заказа. Обычно придерживаются алгоритма, приведенного ниже.

Исходя из величины планируемого потребления стали определяют момент времени (дату), когда уровень запасов стали достигнет гарантийного уровня запасов (в нашем примере – точка В).

От указанного момента времени (даты) отнимают время выполнения заказа (в нашем примере – 30 дней). Полученное число (дата) соответствует моменту времени первого заказа.

На рис. 2.11 представлен график движения запасов листовой стали за январь-июнь в соответствии с планируемым потреблением стали (см. табл. 2.1) и расчетными параметрами. При этом было принято, что в нулевой момент времени уровень запасов стали на складе составлял максимальный желательный запас (22,3т).

Рис. 2.11. График движения запасов листовой стали в системе с фиксированным

интервалом времени между заказами

Следует подчеркнуть, что в системе с фиксированным интерва­лом времени между заказами размер заказа - величина переменная и рассчитывается по формуле (2.10). Так, например, определяем размер первого заказа (P3₁):

Р3₁=МЖЗ-T3₁+ОП = 22,3-14,6+0,38·22=16,06т=23 листа.

Анализ графика показывает, что в апреле и мае образуется 30-дневный дефицит стали. Это вызовет значительные потери производства, связанные с простоем. Такое положение вызвано неравномерностью потребления стали в течение года, а также тем, что в данной системе заказы осуществляются в строго зафиксированные моменты времени. Наряду с этим из-за непостоянства размера заказа могут потребоваться не только различные модели автотранспорта, но и виды транспорта. Так, например, из-за большой величины заказа (более 20-25т) необходимо будет прибегнуть к использованию железнодорожного транспорта.

Таким образом, принимая во внимание низкую эффективность работы данной системы с сырьевыми запасами, отличающимися непостоянством потребления в течение установленного периода, применение системы с фиксированным интервалом времени между заказами для управления запасами листовой стали в соответствии с исходной информацией нецелесообразно с организационно-экономической точки зрения.

Система с установленной периодичностью пополнения запасов до установленного уровня

Система с установленной периодичностью пополнения запасов до установленного уровня является производной от первых двух, рассмотренных выше.

Необходимые параметры для работы этой системы рассчитаны выше в соответствующих системах. Так, пороговый уровень запасов (ПУ) – 10,64т, фиксированный интервал времени между заказами (I) – 53 рабочих дня или 74 календарных дня, максимальный желательный запас (МЖЗ) – 22,3т и гарантийный запас (ГЗ) – 2,28т.

На рис. 2.12 представлен график движения запасов. Видно, что в марте интенсивность потребления стали превышает среднюю расчетную за год (380кг за рабочий день). В этой связи в точке Д

Рис. 2.12. График движения запасов листовой стали в системе с установленной периодичностью пополнения запасов с установленного уровня

делается дополнительный заказ. Его размер определяется по зависимости (2.11):

Р3_д=МЖЗ-ПУ+ОП=22,3-10,64+0,38·22=20т

В точке А2 делается второй основной заказ (Р3₂). Его размер согласно формуле (2.12) составит:

РЗ₂=МЖЗ-ТЗ₂+ОП-РЗ_д=22,3-0,5+0,38·22-20=10,16т

В точке АЗ делается третий основной заказ (Р3₃). Его размер согласно формуле (2.10) составит:

Р3₃=МЖЗ-Т3₃+ОП =22,3-17+0,38·22=13,66т

Анализ рис. 2.12 показывает, что система предусматривает осуще­ствление как основных, так и дополнительных заказов, но не гарантирует бездефицитную работу. Более того, из-за высокой частоты заказов (в период интенсивного потребления товара) имеют место незначительные по величине заказы (Р3₂ = 10,16т), выполнение которых при больших расстояниях транспортировки становится экономически нецелесообразным. В этой связи применение системы управления запасами с установленной периодичностью пополнения запасов до установленного уровня для производственной ситуации в нашем примере является нерациональным решением.

Система «минимум-максимум»

Для работы данной системы управления запасами базовой является система с фиксированным интервалом времени между заказами. Однако заказы осуществляются не через каждый фиксированный интервал времени, а лишь в том случае, если в данный фиксированный момент времени уровень запасов товара на складе равен пороговому уровню запасов или меньше его.

На рис. 2.13 представлен график движения запасов в системе «минимум-максимум». В отличие от графика движения запасов в системе с фиксированным интервалом времени между заказами (см.рис. 2.11), в системе «минимум-максимум» заказ №1 (точка А1) не делается, так как в этот фиксированный момент времени текущий уровень запасов

Рис. 2.13. График движения запасов листовой стали в системе «минимум-максимум»

превышает пороговый уровень (минимум). Первый заказ будет сделан лишь во второй фиксированный момент времени. Поэтому с марта по май образуется более чем двухмесячный дефицит стали. Это указывает на тот факт, что применение системы «минимум-максимум» крайне нецелесообразно для сырьевых (товарных) запасов, имеющих значительное потребление (спрос), а также отличающихся значительными колебаниями потребления (спроса) в течение года или установленного периода времени (сезона).

Не нашли, что искали? Воспользуйтесь поиском: