
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Решение транспортных задач методом потенциалов
Постановка задачи
Имеется L пунктов отправления (складов) – А1, А2, А3,... AL, в которых сосредоточены запасы товаров a1, а2, а3... aL. Кроме того имеется N пунктов потребления – В1, В2, В3,... ВN, потребности каждого из которых в1, в2, в3... вN.
Перед тем как приступить к решению, необходимо, чтобы было выполнено равенство

Если равенство выполняется, транспортная задача - закрытая, если нет – открытая. Должны быть известны стоимости перевозки из i-го пункта Аi в k-й пункт Вk (Cik).
Требуется найти оптимальный план перевозок, т.е. рассчитать, какое количество продукции необходимо отправить из пунктов отправления в пункты назначения, чтобы стоимость перевозок была минимальной.
Общий алгоритм
Составляется начальный план перевозок. Для этого заполняются клетки плана, где наименьшая стоимость перевозки. При этом придерживаются следующего правила: на каждом шаге или исчерпываем запас соответствующего пункта отправления, или удовлетворяем потребность соответствующего пункта назначения.
Условие задачи. Необходимо отправить автомобили из трех баз в четыре магазина. На базах A1, А2, А3 имеется соответственно 50, 30, 40ед. товара. Спрос магазинов В1, В2, В3, В4 – соответственно 50, 10, 40, 20ед. товара.
Равенство запасов на базах и потребностей магазинов для данной задачи выполняется. Можем приступать к решению. Составляем, согласно правилу, следующую матрицу (табл. 8.16). В правом ни жнем углу ячейки указана стоимость перевозки единицы товара (тыс.руб.) из соответствующей базы в соответствующий магазин.
Таблица 8.16
Исходный план грузоперевозок
| в1 | в2 | в3 | в4 | Запас | Потенциал | |
| А1 А2 А3 Спрос Потенциал | 30 1 20 5 β1 | 10 1 β2 | 40 1 β3 | 10 2 10 2 β4 | а1 а2 а3 |
Вычисляем стоимость перевозки:
S=30∙1+20∙5+10∙1+40∙1+10∙2+10∙2=220тыс.руб.
Нужно проверить, насколько оптимален такой план. Для этого используется метод потенциалов, который состоит в следующем. Необходимо, во-первых, определить величину потенциалов а1, а2, а3 и β1, β2, β3, β4. Для этого составляется система уравнений для занятых клеток:

Итак,
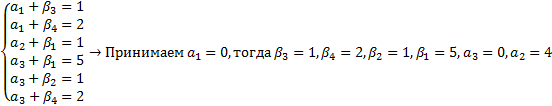
Используя расчетные величины потенциалов, определяем их суммы для соответствующих незанятых клеток и сравниваем с размером стоимости перевозки для данной клетки. Если эта сумма больше, план не является оптимальным.






Для улучшения плана в клетке, где условие не выполняется, число следует увеличить до максимально возможного значения, которое обозначаем буквой Z (табл. 8.17).
Таблица 8.17
Улучшенный план грузоперевозок
| в1 | в2 | в3 | в4 | Запас | Потенциал | |
| А1 А2 А3 Спрос Потенциал | Z=10 4 30 1 20 5 β1 | 10 1 β2 | 40 1 β3 | 20 2 β4 | а1 а2 а3 |
Затем вновь определяем потенциалы, записав систему уравнений для занятых клеток. Проверяем условие для незанятых клеток и видим, что все условия выполняются. Следовательно, план является оптимальным.
Рассчитываем стоимость перевозки:
S=10∙4+30∙1+10∙5+10∙1+40∙1+20∙2=210тыс.руб.
Задача решена.
Если мы имеем дело с открытой транспортной задачей, ее необходимо преобразовать в закрытую.
1. Рассмотрим случай, когда запас превышает спрос. Для этого в плане предусматривается фиктивный пункт назначения, для которого спрос равен разности между общим запасом и действительным спросом:

Все затраты на доставку груза в этот фиктивный пункт назначения принимаются равными нулю, поэтому целевая функция (S) не изменится. Груз, который, согласно полученному решению, нужно отправить в фиктивный пункт назначения, на самом деле останется на месте.
2. Если спрос превышает предложение, вводится фиктивный пункт отправления, запас которого равен разности общего действительного спроса и общего действительного запаса:

Затраты на доставку из этого пункта равны нулю, поэтому целевая функция (S) не изменится, а груз из фиктивного пункта отправления на самом деле никуда не поступает.
Следует отметить, что основной недостаток классических транспортных задач (при реализации на практике) заключается в сложности определения стоимости перевозки единицы товара из соответствующей базы в соответствующий магазин.
Не нашли, что искали? Воспользуйтесь поиском: