
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Оптимизация маятниковых маршрутов с обратных
Холостым пробегом
Другим важным направлением повышения эффективности использования транспорта на маятниковых маршрутах с обратным холостым пробегом является их оптимизация.
Методику оптимизации маятниковых маршрутов с обратным холостым пробегом рассмотрим на примере следующей производственной ситуации. В соответствии с заключенными договора
и на оказание транспортных услуг автотранспортное предприятие (АТП) 24.02.2012 г. должно было обеспечить доставку песка четырем потребителям – П1, П2, П3 и П4, потребности которых составляют соответственно 20, 30, 35 и 40м3. При этом оговорено, что доставка должна быть обеспечена независимо от времени рабочего дня. Расстояния в километрах пути между АТП и потребителями, а также между потребителями и карьером (К), откуда будет осуществляться доставка песка, представлены на схеме (рис. 8.6).
Следует отметить, что при составлении этой схемы наряду с обеспечением минимального расстояния между соответствующими пунктами необходимо учитывать следующие факторы: фактическое состояние дорожного покрытия, количество возможных кратковременных остановок, регламентированных правилами дорожного движения, и т.п. Это позволит, с одной стороны, сократить физический износ техники в результате ее производственной эксплуатации, с другой – повысить производительность автотранспорта. Так, в нашем примере (рис. 8.6) длина груженой ездки от точки К до П4 составляет 19км, что больше суммы первого и второго нулевых пробегов (6+12=18км) и обусловлено учетом указанных выше факторов.

Рис. 8.6. Схема взаимного размещения автотранспортного предприятия (АТП), карьера (К) и потребителей (П)
Транспортировка груза в соответствии с договорами будет осуществляться автомобилями МАЗ 5551 с емкостью грузовой платформы 5м3. В этой связи в пункт II, потребуется сделать 4 ездки (20м3:5м3), в пункты П2, П3 и П4 – 6, 7 и 8 ездок соответственно. Наряду с этим было принято, что время работы автомобилей в наряде – 8ч, техническая скорость – 40км/ч, а суммарное время (простой) под погрузкой-разгрузкой – 15мин.
Так как договоры заключаются с каждым потребителем отдельно, для каждого потребителя требуется определить необходимое количество автомобилей для его обслуживания, а также путь, который проходит это количество автомобилей.
Для обслуживания потребителя, например, за 8-часовой рабочий день может потребоваться один автомобиль и более. Поэтому, во-первых, необходимо определить то количество автомобилей, которое нужно для обслуживания потребителя за время работы в наряде (8ч) по формуле:


Полученное количество автомобилей округляется в большую сторону до целого числа.
Так, необходимое количество автомобилей для первого потребителя (П1) составит:

Рассчитанное дробное число (0,6) округляется в большую сторону До целого числа – 1автомобиль.
Необходимое количество автомобилей для второго потребителя (П2):

Полученное дробное число (0,61) округляется в большую сторону до целого числа – 1 автомобиль.
Необходимое количество автомобилей для третьего потребителя (П3):

Рассчитанное дробное число (0,53) округляется в большую сторону до целого числа – 1автомобиль.
Необходимое количество автомобилей для четвертого потребителя (П4):

Полученное дробное число (0,89) округляется в большую сторону до целого числа – 1 автомобиль.
Путь, который проходят автомобили (полученное количество автомобилей) при обслуживании соответствующего потребителя определяется по формуле



Так, путь, который проходит полученное количество автомобилей (1 автомобиль) для обслуживания первого потребителя, составит:

Путь, который проходит полученное количество автомобилей (1 автомобиль) для обслуживания второго потребителя, составит:

Путь, который проходит необходимое количество автомобилей (1 автомобиль) для обслуживания третьего потребителя, составит:

Путь, который проходит необходимое количество автомобилей (1 автомобиль) для обслуживания четвертого потребителя, составит:

Результаты представленных выше расчетов отмечаются в соответствующих договорах на обслуживание потребителей и являются доходной базой для расчета стоимости транспортных услуг для каждого потребителя. Таким образом, совокупный дневной пробег автомобилей по обслуживанию четырех потребителей, согласно договорам, составит 592км∙(151+136+99+206 км).
Задача оптимизации транспортных маршрутов заключается в том, чтобы обеспечить минимально необходимый пробег автомобилей при обслуживании потребителей. Анализ исходной информации и рис. 8.6 показывает, что совокупный груженый пробег автомобилей оптимизировать невозможно, так как количество ездок, которые необходимо сделать потребителям, а также расстояния от карьера до пунктов назначения строго зафиксированы договорными обязательствами. Следовательно, оптимизация маятниковых маршрутов возможна только за счет минимизации совокупного порожнего пробега. Это достигается с одновременным учетом второго нулевого и холостого пробегов автотранспорта для соответствующих потребителей. Так, например, в нашем примере потребитель П2 отличается минимальным вторым нулевым пробегом (9км). Однако максимальный холостой пробег имеет место при обслуживании потребителя П3 (холостой пробег=груженой ездке=19км). В этой связи, чтобы учесть влияния этих двух показателей, необходимо определить их разность для всех потребителей.
Таким образом, минимизация совокупного порожнего пробега возможна в случае выполнения следующих двух условий.
1. Построение маршрутов по обслуживанию потребителей (пунктов назначения) необходимо осуществлять таким образом, чтобы в пункте назначения, который имеет минимальную разность расстояния от него до автотранспортного предприятия и расстояния от товарной базы (в нашем случае – карьера) до этого пункта назначения (разность второго нулевого пробега и груженой ездки), заканчивало свою дневную работу, возвращаясь на автотранспортное предприятие, максимально возможное количество автомобилей. При этом максимальное количество определяется количеством ездок, которые необходимо сделать в этот пункт назначения. Так, если общее число автомобилей по обслуживанию всех потребителей равно или меньше количества ездок, которое необходимо сделать в указанный пункт назначения, то все эти автомобили проедут через данный пункт назначения, сделав последнюю груженую ездку в конце рабочего дня при возвращении на АТП. В противном случае, если общее количество автомобилей по обслуживанию всех потребителей больше количества ездок, которое необходимо сделать в указанный пункт назначения, то автомобили, которые входят в превышающее число, должны заканчивать свою дневную работу в пункте назначения, имеющем следующее по величине минимальное значение разности второго нулевого пробега и груженой ездки, и т.д.
2. Общее количество автомобилей, работающих на всех маршрутах при обслуживании потребителей, должно быть минимально необходимым. Это достигается обеспечением максимально полной загрузки автомобилей по времени в течение рабочего дня (например, 8-часовой рабочей смены).
С учетом представленных выше условий запишем структурную математическую модель оптимизации маятниковых маршрутов:

при условиях:
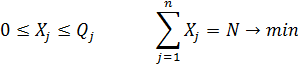
где L – совокупный порожний пробег, км; j – номер потребителя; n – количество потребителей;  – расстояние от пункта назначения (Пj) до автотранспортного предприятия (второй нулевой пробег), км;
– расстояние от пункта назначения (Пj) до автотранспортного предприятия (второй нулевой пробег), км;  – расстояние от товарной базы (в нашем случае – карьера К) до пункта назначения (Пj) (груженая ездка), км; Xj – количество автомобилей, работающих на маршрутах с последним пунктом разгрузки (Пj); (Qj – необходимое количество ездок в пункт назначения (Пj); N – общее количество автомобилей, работающих на всех маршрутах.
– расстояние от товарной базы (в нашем случае – карьера К) до пункта назначения (Пj) (груженая ездка), км; Xj – количество автомобилей, работающих на маршрутах с последним пунктом разгрузки (Пj); (Qj – необходимое количество ездок в пункт назначения (Пj); N – общее количество автомобилей, работающих на всех маршрутах.
Используется следующий алгоритм решения подобных задач.
1. Составляется рабочая матрица №1 (табл. 8.4).
Выбирают пункт, имеющий минимальную оценку (разность расстояний). В нашем примере это пункт назначения П1
2. Учитывая исходную информацию, определяют общее количество автомобилей (N) до оптимизации, работающих на всех маршрутах. Для этого нужно сложить количество автомобилей (до округления) для соответствующих потребителей. В нашем примере эта сумма составит 2,63 автомобиля (0,6+0,61+0,53+0,89). Полученная сумма округляется в большую сторону до целого числа. Это число и есть «необходимое количество машин до оптимизации». В нашем примере – 2,63 → 3 автомобиля.
Таблица 8.4
Исходная рабочая матрица №1
| Пункт назначения | Исходные данные | Оценка (разность расстояний) |
| Пj П1 П2 П3 П4 |   Qj
12 19
9 11
15 6
20 12
Qj
12 19
9 11
15 6
20 12
|  -7
-2
-7
-2
|
3. В соответствии с первым условием обеспечения минимизации совокупного порожнего пробега устанавливается количество автомобилей, которое проедет через выбранный пункт назначения (см. п.1 алгоритма), осуществляя последнюю груженую ездку в конце рабочего дня при возвращении на АТП. В нашем примере это пункт назначения П1. Так как общее количество автомобилей по обслуживанию потребителей П1, П2, П3 и П4 равно трем (меньше необходимого количества ездок, которое нужно сделать в пункт назначения П1), то на данном пункте будут заканчивать свою дневную работу все три автомобиля, причем в П1, один из автомобилей сделает две груженые ездки.
4. Определяется маршрут движения для первого автомобиля. Для этого выбирают два пункта, имеющие минимальную и наибольшую оценку (разность расстояний). В нашем случае это соответственно «-7» (П1) и 9 (П3). Исходя из первого условия, автомобиль, обслуживающий эти пункты назначения, начинает рабочую смену с пункта П3и заканчивает пунктом П1.
5. Определяют, какое количество груженых ездок сможет сделать автомобиль в пункты назначения первого маршрута за 8-часовой рабочий день.
Из представленных выше рассуждений (см. п. 3 алгоритма) допускаем, что на первом маршруте в пункт назначения П1 будет сделана 1 груженая ездка. В этой связи остается определить, сколько ездок успеет сделать автомобиль в пункт П3.
Для этого рассчитывают поминутное время работы первого автомобиля на маршруте.
Время в пути от Г до К = (l гк/υт)∙60мин.=(6/40)∙60=9мин.
Время в пути от П1 до Г = (12/40)∙60=18мин.
Время оборота КП3К=((6+6)/40)∙60+15=33мин.
Время в пути КП1=(19/40)∙60+15=43,5мин.
Здесь 15мин – суммарное время для погрузи-разгрузки.
Определяем, сколько ездок сделает автомобиль в пункт П3, учитывая, что время его работы в наряде составляет 480мин:
(480-9-43,5-18)/33=12,4 ездки.
Однако в пункт П3, согласно договору, нужно сделать 7 ездок. Это обстоятельство обусловливает необходимость догрузки первого автомобиля по времени рабочей смены. Допустим, что наряду с обслуживанием пунктов П1 и П3 автомобиль будет также обслуживать пункт П4. Определяем, сколько ездок успеет осуществить автомобиль в пункт П4. Для этого рассчитаем время оборота КП4К. Оно составит 51 мин ([(12+12)/40]∙60+15).
Тогда количество ездок в пункт П4:
(480-9-7∙33-43,5-18)/51=3,5≈3 ездки.
Цикл повторяется. Составляют вторую рабочую матрицу с учетом выполненной работы на первом маршруте. В нашем примере в пункт назначения П1 сделана 1 ездка, в пункт П3 – 7 ездок (дневные потребности удовлетворены), а в пункт П4 – 3 ездки (табл. 8.5).
Таблица 8.5
Рабочая матрица №2
| Пункт назначения | Исходные данные | Оценка (разность расстояний) |
| Пj П1 П2 П4 |   Qj
12 19
3=4-1
9 11
20 12
5=8-3
Qj
12 19
3=4-1
9 11
20 12
5=8-3
|  -7
-2
-7
-2
|
Определяют маршрут движения для второго автомобиля. В нашем примере (принимая во внимание пункты 3 и 4 алгоритма) очевидно, что маршрут движения второго автомобиля будет проходить через пункты назначения II1, П2, П4. В начале рабочего дня второй автомобиль сделает 5 ездок в пункт П4 (таким образом, дообслужив его), начнет обслуживание пункта П2 и так же, как первый автомобиль, сделает в конце рабочего дня 1 груженую ездку в пункт П1 и возвратится на АТП. Из этого следует, что необходимо определить, сколько ездок осуществит (успеет осуществить) второй автомобиль в пункт П2.
Рассчитаем поминутно время работы на маршруте движения второго автомобиля.
Время в пути от Г до К=(l гк/υт)∙60мин=(6/40)∙60=9мин.
Время в пути от П1 до Г=(12/40)∙60=18мин.
Время пяти оборотов КП4К=5∙[((12+12)/40)∙60+15]=255мин.
Время оборота КП2К=((11+11)/40)∙60+15=48мин.
Время в пути KП1=(19/40)∙60+15=43,5мин.
Определяем, сколько ездок сделает второй автомобиль в пункт П2, учитывая, что время его работы в наряде составляет 480мин:
(480-9-255-43,5-18)/48=3,2≈3 ездки.
Цикл повторяется. Составляют третью рабочую матрицу с учетом выполненной работы на первом и втором маршрутах. В нашем примере в пункт назначения П1 сделано 2 ездки, в пункт П2 – 3 ездки, для пунктов П3, П4 дневные потребности удовлетворены (табл. 8.6).
Таблица 8.6
Рабочая матрица №3
| Пункт назначения | Исходные данные | Оценка (разность расстояний) |
| Пj П1 П2 |   Qj
12 19
2=4-2
9 11
3=6-3
Qj
12 19
2=4-2
9 11
3=6-3
|  -7
-2
-7
-2
|
Определяют маршрут движения для третьего автомобиля Анализ табл. 8.6 показывает, что его маршрут движения будет проходить через пункты назначения П2, П1. В начале рабочего дня третий автомобиль сделает 3 ездки в пункт П2, а в конце рабочего дня – 2 груженые ездки в пункт П1 и возвратится на АТП.
Сравнивая маршрут движения третьего автомобиля с маршрутом движения второго, можно с уверенностью сказать, что третий автомобиль будет иметь определенную недогрузку по времени рабочей смены.
Определим ее величину. Для этого рассчитаем поминутно время работы на маршруте движения третьего автомобиля.
Время в пути от Г до К=(l гк/υт)∙60мин=(6/40)∙60=9мин.
Время в пути от П1 до Г=(12/40)∙60=18мин.
Время трех оборотов КП2К=3∙[((11+11)/40)∙60+15]=144мин.
Время в пути КП1KП1=((19+19+19)/40)∙60+2∙15=115,5мин.
Величина недогрузки по времени рабочей смены третьего автомобиля составит:
480-9-144-115,5-18=193,5мин≈3,2ч.
Величина недогрузки по времени рабочей смены третьего автомобиля позволяет при необходимости направить его на выполнение другой транспортной работы.
Составляют сводную маршрутную ведомость (табл. 8.7).
Таблица 8.7
Сводная маршрутная ведомость
| № маршрута | последовательность выполнения маршрута | Расшифровка | Количество автомобилей на маршруте | Длина маршрута в км |
| Г→К→П3→К→ П3→К→П3→К→П3 →К→П3→К→П3 →К→П3→К→П4 →К→П4→К→П4 →К→П1→Г | Г – АТМ К – карьера П3 – ПМК П4 – ДРСУ П1 – ЖБИ | |||
| Г→К→П4→К→П4 →К→П4→К→П4→К →П4→К→П2→К→ П2→К→П2→К→П1→Г | Г – АТМ К - карьера П4 – ДРСУ П2 – РСУ П1 – ЖБИ | |||
| Г→К→П2→К→П2 →К→П2→К→П1 →К→П11→Г | Г – АТМ К - карьера П2 – РСУ П1 – ЖБИ |
Анализ табл. 8.7 показывает, что совокупный дневной пробег трех автомобилей в соответствии с проведенными оптимизационными расчетами составляет 557км, что на 35км (592-557км), или на 6%, меньше по сравнению с традиционным порядком обслуживания (до оптимизации).
Анализ алгоритма и порядок оптимизации маятниковых маршрутов с обратным холостым пробегом указывают на высокую трудоемкость расчетных работ, что не позволяет в должной мере использовать подобный подход на практике.
В связи с этим был разработан программный продукт, который позволяет осуществлять оптимизацию маятниковых маршрутов с обратным холостым пробегом с помощью компьютерной техники. Это дает возможность снижать трудоемкость расчетных работ в десятки раз, обеспечивая тем самым привлекательность программы для повсеместного внедрения в практику хозяйственной деятельности не только автотранспортных предприятий, но и других организаций, осуществляющих грузоперевозки, в том числе внутрихозяйственные.
Программа дает возможность оптимизировать маршруты по обслуживанию до восьми потребителей посредством автотранспорта или тракторно-транспортных агрегатов в количестве не более восьми единиц, имеющих одинаковые технико-эксплуатационные показатели: грузоподъемность (объем грузовой платформы) и скорость движения.
Выходной Продукцией программы является маршрутная ведомость, устанавливающая не только последовательность движения автомобилей на маршрутах, но и протяженность, продолжительность каждого маршрута. Наряду с этим программа показывает необходимое количество единиц транспортных средств, а также их совокупный пробег до оптимизации и после нее, что позволяет определять экономический эффект от использования оптимальной маршрутизации.
Рассмотрим реализацию предлагаемого программного продукта на представленном выше примере, используя следующий алгоритм.
С учетом исходной информации заполняют зеленые области таблицы листа «план» – это ячейки СЗ-С10, D3-D10, ЕЗ-Е10, С13, D13, Е13, G13, Н13 (табл. 8.8). Синие области таблицы (КЗ-К10, К13, К14; L3-L10, L13, L14) не заполняются. Они рассчитываются программой согласно формулам (8.1), (8.2).
После заполнения таблицы на листе «План» необходимо нажать кнопку «Оптимизация». Программа, выполнив оптимизационный расчет, в результате представляет на листе «Маршрут» маршрутную ведомость движения автомобилей (М1-М8).
Таблица 8.8
Таблица листа «План»
| B | C | D | E | G | H | K | L | |
| Потребитель | Потребность, м3(т) | Груженая ездка, км | Второй нулевой пробег, км | Количество автомобилей для обслуживания потребителя | Пробег для обслуживания потребителя | |||
| П1 | ||||||||
| П2 | ||||||||
| П3 | ||||||||
| П4 | ||||||||
| П5 | ||||||||
| П6 | ||||||||
| П7 | ||||||||
| П8 | ||||||||
| До/после оптимизации | ||||||||
| Грузоподъемность, м3(т) | Средняя техническая скорость, км/ч | Суммарный простой под погр.-разгр., ч | Время работы в наряде, ч | Первый нулевой пробег, км | Необходимо машин | Совокупный пробег по маршрутах, км | ||
| Транспорт | 0,25 | |||||||
В нашем примере в результате оптимизации получено, что для обслуживания четырех потребителей нужны три автомобиля, маршруты движения которых представлены в табл. 8.9. Следует отметить, что буквой А обозначается автотранспортное предприятие (место ночной стоянки), буквой Б – товарная база, буквой П (П1, П2, ПЗ и П4) – потребители.
Таблица 8.9
Маршрутная ведомость
| М1 | км | М2 | км | М3 | км | ||||||
| км | время | 0:00 | км | время | 0:00 | км | время | 0:00 | |||
| А-Б | 0:09 | 0:09 | А-Б | 0:09 | 0:09 | А-Б | 0:09 | 0:09 | |||
| Б-П2 | 0:31 | 0:40 | Б-П1 | 0:43 | 0:52 | Б-П4 | 0:33 | 0:42 | |||
| П2-Б | И | 0:16 | 0:57 | П1-Б | 0:28 | 1:21 | П4-Б | 0:18 | 1:00 | ||
| Б-П2 | 0:31 | 1:28 | Б-П2 | 0:31 | 1:52 | Б-П4 | 0:33 | 1:33 | |||
| П2-Б | И | 0:16 | 1:45 | П2-Б | И | 0:16 | 2:09 | П4-Б | 0:18 | 1:51 |
Окончание таблицы 8.9
| Б-П2 | 0:31 | 2:16 | Б-П2 | И | 0:31 | 2:40 | Б-П4 | 0:33 | 2:24 | ||
| П2-Б | 0:16 | 2:33 | П2-Б | 0:16 | 2:57 | П4-Б | 0:18 | 2:42 | |||
| Б-ПЗ | 0:24 | 2:57 | Б-П2 | 0:31 | 3:28 | Б-П4 | 0:33 | 3:15 | |||
| ПЗ-Б | 0:09 | 3:06 | П2-Б | 0:16 | 3:45 | П4-Б | 0:18 | 3:33 | |||
| Б-ПЗ | 0:24 | 3:30 | Б-П1 | 0:43 | 4:28 | Б-П4 | 0:33 | 4:06 | |||
| ПЗ-Б | 0:09 | 3:39 | П1-А | 0:18 | 4:46 | П4-Б | 0:18 | 4:24 | |||
| Б-ПЗ | 0:24 | 4:03 | Б-П4 | 0:33 | 4:57 | ||||||
| ПЗ-Б | 0:09 | 4:12 | П4-Б | 0:18 | 5:15 | ||||||
| Б-ПЗ | 0:24 | 4:36 | Б-П4 | 0:33 | 5:48 | ||||||
| ПЗ-Б | 0:09 | 4:45 | П4-Б | 0:18 | 6:06 | ||||||
| Б-ПЗ | 0:24 | 5:09 | Б-П4 | 0:33 | 6:39 | ||||||
| ПЗ-Б | 0:09 | 5:18 | П4-Б | 0:18 | 6:57 | ||||||
| Б-ПЗ | 0:24 | 5:42 | Б-П1 | 0:43 | 7:40 | ||||||
| ПЗ-Б | 0:09 | 5:51 | П1-А | 0:18 | 7:58 | ||||||
| Б-ПЗ | 0:24 | 6:15 | |||||||||
| ПЗ-Б | 0:09 | 6:24 | |||||||||
| Б-П1 | 0:43 | 7:07 | |||||||||
| П1-А | 0:18 | 7:25 |
Анализ маршрутной ведомости показывает, что соответствующий маршрут представляет собой последовательное выполнение отдельным автомобилем отрезков пути (А-Б, Б-П2 и т.д.).
При этом для каждого отрезка указываются:
- протяженность;
- продолжительность времени для его прохождения;
- время окончания его прохождения с начала смены.
Важно подчеркнуть, что продолжительность времени для прохождения груженой ездки (например, Б-П2) включает не только время на преодоление пути (11км), но и суммарный простой автомобиля под погрузкой-разгрузкой.
Наряду с этим для каждого маршрута указывают его протяженность и продолжительность выполнения. Так, для маршрута Ml протяженность составляет 187 км, а продолжительность выполнения – 7ч 25мин.
Сравнение маршрутных ведомостей (табл. 8.7 и 8.9) показывает, что они различаются. При этом не различается лишь та область маршрутов, которая несет в себе суть оптимизации маятниковых маршрутов с обратным холостым пробегом. Она заключается в том, что на потребителе (П1), который имеет минимальную разность второго нулевого пробега и груженой ездки, заканчивают свою дневную работу все три автомобиля. Неизменным оказался также совокупный путь автомобилей на трех маршрутах после оптимизации - 557 км (ячейка L14 листа «План»),
Этот факт указывает на то, что маршрутная ведомость может изменяться в соответствии с дополнительными договорными обязательствами (например, доставка определенной части груза строго «до обеда»). Однако при этом неизменной должна оставаться точка (потребитель) последней разгрузки автомобилей в конце рабочего дня согласно табл. 8.9.
Таким образом, внедрение предлагаемой компьютерной программы в практику хозяйственной деятельности позволит при одних и тех же объемах грузоперевозок, с одной стороны, повысить доходность обслуживающих автотранспортных предприятий или сократить издержки, связанные с внутрипроизводственными транспортными расходами, в других организациях, с другой – снизить потребление энергоресурсов, что весьма актуально в настоящее время, в условиях постоянного повышения цен на энергоносители.
Не нашли, что искали? Воспользуйтесь поиском: