Метод Остроградского

метод выделения рациональной части неопределенного интеграла от рациональной дроби, знаменатель которой — многочлен степени n с кратными корнями, а числитель — многочлен степени m n-1. Согласно этому методу, 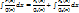, где многочлены Q₁, Q₂, P₁, P₂ имеют степени соответственно n₁, n₂, m₁, m₂, такие что n₁ + n₂ = n, m₁ n₁ — 1, m₂ n₂ — 1 и многочлен Q₂(x) не имеет кратных корней. Таким образом, Q₁(x) является наибольшим общим делителем многочленов Q(x) и 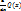, следовательно, его можно найти, используя алгоритм Евклида. Из этого равенства, дифференцируя, получаем тождество, которое позволяет найти явное выражение многочленов P₁(x) и P₂(x).

Не нашли, что искали? Воспользуйтесь поиском: