
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Дифференциальное исчисление.
Определение производной
Производная 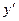 или
или 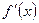 от данной функции
от данной функции 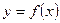 есть предел отношения приращения функции к соответствующему приращению аргумента, когда приращение аргумента стремится к нулю:
есть предел отношения приращения функции к соответствующему приращению аргумента, когда приращение аргумента стремится к нулю:  или
или  .
.
Для вычисления производной элементарной функции используются следующие формулы, полученные с помощью определения производной.
1) Производная постоянной равна нулю.
2) 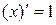 .
.
3)  .
.
4)  , где
, где 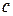 – постоянная.
– постоянная.
Формулы 3 и 4 можно записать одной равносильной им формулой  , где
, где 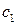 и
и  - постоянные.
- постоянные.
Свойство производной, выраженное этой формулой, называется свойством линейности. В частном случае, если 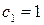 ,
, 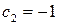 , получим, что
, получим, что
 ,
,
т.е. производная разности двух функций равна разности производных этих функций.
5) 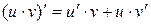 .
.
6) 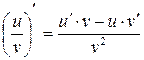 .
.
7) 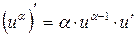 , где
, где 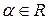 .
.
8) 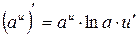 , где
, где 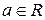 и
и 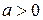 .
.
Если  , то
, то 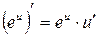 , так как
, так как  .
.
9)  , где
, где 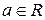 ,
, 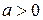 и
и 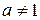 .
.
Если  , то
, то 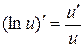 .
.
10) 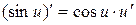 .
.
11)  .
.
12) 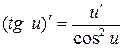 .
.
13) 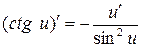 .
.
14) 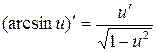 .
.
15) 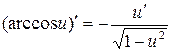 .
.
16)  .
.
17)  .
.
Пример 17:
а) 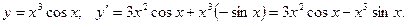
б) 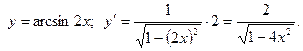
в) 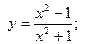
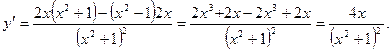
Производные высших порядков.
Производная второго порядка функции 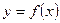
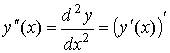
Пример 18.
а) Найти производную второго порядка функции  .
.
Решение. Найдем сначала производную первого порядка 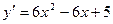 .
.
От производной первого порядка возьмем еще раз производную 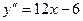 .
.
б) Найти производную третьего порядка функции  .
.
Решение. 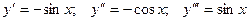 .
.
Исследование функций.
План полного исследования функции:
1. Элементарное исследование:
- найти область определения и область значений;
- выяснить общие свойства: четность(нечетность), периодичность;
- найти точки пересечения с осями координат;
- определить участки знакопостоянства.
2. Асимптоты:
- найти вертикальные асимптоты 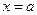 , если
, если  ;
;
- найти наклонные асимптоты:  .
.
Если  любое число, то
любое число, то 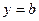 – горизонтальные асимптоты.
– горизонтальные асимптоты.
3. Исследование с помощью 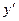 :
:
- найти критические точки, те. точки в которых 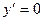 или не существует;
или не существует;
- определить интервалы возрастания, те. промежутки, на которых 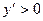 и убывания функции –
и убывания функции –  ;
;
- определить экстремумы: точки, при переходе через которые 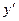 меняет знак с «+» на «–», являются точками максимума, с «–» на «+» – минимума.
меняет знак с «+» на «–», являются точками максимума, с «–» на «+» – минимума.
4. Исследование с помощью  :
:
- найти точки, в которых  или не существует;
или не существует;
- найти участки выпуклости, т.е. промежутки, на которых  и вогнутости –
и вогнутости – 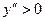 ;
;
- найти точки перегиба, т.е. точки при переходе через которые  меняет знак.
меняет знак.
5. Построение графика функции.
Пример 19. Исследовать функцию и построить ее график.
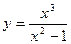 .
.
1) 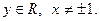
2) Функция нечетная: 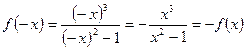 .
.
3) Асимптоты.
 – вертикальные асимптоты, т.к.
– вертикальные асимптоты, т.к. 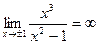
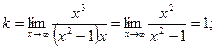
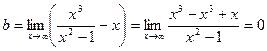
Наклонная асимптота  .
.
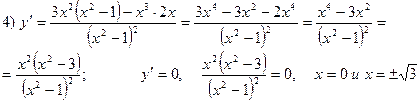
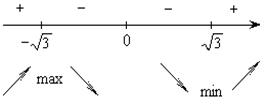
5) 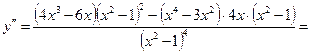
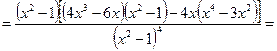
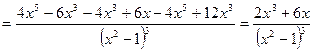
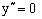

 – точка перегиба.
– точка перегиба.
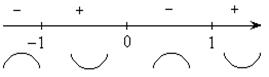
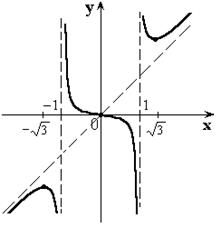
Схематичный график данной функции:
Правило Лопиталя.
Теорема. Предел отношения двух бесконечно малых или бесконечно больших функций равен пределу отношения их производных (конечному или бесконечному), если последний существует в указанном смысле.
Т.е. при раскрытии неопределенностей вида 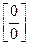 или
или 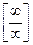 можно использовать формулу:
можно использовать формулу: 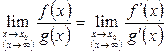 .
.
Пример 19.
а) 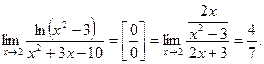
б) 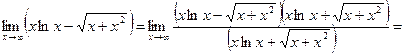
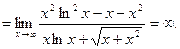
Не нашли, что искали? Воспользуйтесь поиском: