Неопределенный интеграл

Определение 1. Функция называется первообразной для 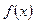, если .

Определение 2. Неопределенным интегралом от функции f(x) называется совокупность всех первообразных для этой функции.

Обозначение: , где c - произвольная постоянная.

Свойства неопределенного интеграла

1. Производная неопределенного интеграла:

2. Дифференциал неопределенного интеграла: .

3. Неопределенный интеграл от дифференциала: .

4. Неопределенный интеграл от суммы (разности) двух функций:

;

5. Вынесение постоянного множителя за знак неопределенного интеграла:

Таблица неопределенных интегралов

1)

2)

3)

Если , то .

4)

5)

6)

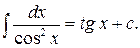
7)

8)

9)

10)

11)

Все формулы справедливы также в случае, если переменную заменить на некоторую другую функцию. Так, если в формуле 2 заменить на , то получим, что

.

Основные методы интегрирования

1. Использование свойств неопределенного интеграла.

Пример 25.

2. Подведение под знак дифференциала.

Пример 26.

3. Метод замены переменной:

а) замена в интеграле :

, где

- функция, интегрируемая легче, чем исходная;

- функция, обратная функции ;

- первообразная функции .

Пример 27.

б) замена в интеграле вида:

;

Пример 28.

Пример 29.

4. Метод интегрирования по частям:

Пример 30.

Пример 31.

Возьмем отдельно интеграл

Вернемся к нашему интегралу:

Не нашли, что искали? Воспользуйтесь поиском: