
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Схема исследования на экстремум функции двух переменных.
1. Найти частные производные функции 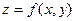 :
:  и
и  .
.
2. Решить систему уравнений  ,
, 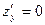 и найти критические точки функции.
и найти критические точки функции.
3. Найти частные производные второго порядка, вычислить их значения в критических точках и с помощью достаточного условия сделать вывод о наличии экстремумов.
4. Найти экстремумы функции.
Пример 23. Найти экстремумы функции  .
.
Решение.
1) Найдем частные производные  .
.
2) Решим систему уравнений 

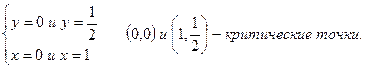
3) Найдем частные производные второго порядка и их значения в критических точках:  . В точке
. В точке  получим:
получим:  значит, в точке
значит, в точке  экстремума нет. В точке
экстремума нет. В точке  получим:
получим:  значит, в точке
значит, в точке  минимум.
минимум.
4) 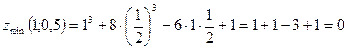 .
.
Ответ. 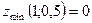
Глобальный экстремум (наибольшее и наименьшее значение функции).
Наибольшее и наименьшее значения функции нескольких переменных, непрерывной на некотором замкнутом множестве, достигаются или в точках экстремума, или на границе множества.
Схема нахождения наибольшего и наименьшего значений.
1) Найти критические точки, лежащие внутри области, вычислить значение функции в этих точках.
2) Исследовать функцию на границе области; если граница состоит из нескольких различных линий, то исследование необходимо провести для каждого участка отдельно.
3) Сравнить полученные значения функции и выбрать наибольшее и наименьшее.
Пример 24. Найти наибольшее и наименьшее значения функции  в прямоугольнике
в прямоугольнике 
 .
.
Решение. 1) Найдем критические точки функции, для этого найдем частные производные: 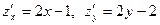 , и решим систему уравнений:
, и решим систему уравнений:

Получили критическую точку A  . Полученная точка лежит внутри заданной области.
. Полученная точка лежит внутри заданной области.


y 2
 B C
B C
. A
 0 D x
0 D x
Границу области составляют четыре отрезка:  и
и  . найдем наибольшее и наименьшее значение функции на каждом отрезке.
. найдем наибольшее и наименьшее значение функции на каждом отрезке.

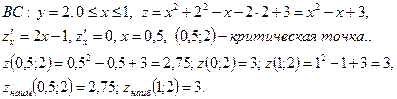

4) Сравним полученные результаты и получим, что 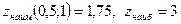 в точках
в точках 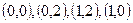 .
.
Не нашли, что искали? Воспользуйтесь поиском: