
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Яхьев Н.Я. Основы теории надежности и диагностика [Текст]: учебник / Н.Я. Яхьев, А.В. Кораблин. - М.: ИЦ «Академия», 2009. - 256 с.
Нормативная литература
21. ГОСТ 11.006-74 Прикладная статистика. Правила проверки согласия опытного распределения [Текст]: / М.: изд. стандартов, 1992. - 19 с.
22. ГОСТ 21624-81 Система технического обслуживания и ремонта автомобильной техники. Требования к эксплуатационной технологичности и ремонтопригодности изделий [Текст]: / М.: изд. стандартов, 1982. - 14 с.
23. ГОСТ 23.220-84 Обеспечение износостойкости изделий. Методы оценки истирающей способности поверхностей восстановленных валов [Электронный ресурс]. − Режим доступа: http: standartgost.ru/ГОСТ23.220-84#page1
24. ГОСТ 23.224 Обеспечение износостойкости изделий. Метод оценки износостойкости восстанавливаемых изделий [Электронный ресурс]. − Режим доступа: http://vsegost.com/Catalog/22/2261.shtml
25. ГОСТ 27.002-89 Надежность в технике. Термины и определения [Электронный ресурс]. − Режим доступа: http: //www.i-mash.ru/2008/07/22/gost_270089.html
26. ГОСТ 27674-88 Трение, изнашивание и смазка. Термины и определения [Текст]: / М.: изд. стандартов, 1992. - 19 с.
27. ГОСТ 27860-88 Детали трущихся сопряжений. Методы измерения износа [Электронный ресурс]. − Режим доступа: http://www.ankera.ru/gost_28781.html
28. Положение о техническом обслуживании и ремонте подвижного состава автомобильного транспорта [Текст]: / Минавтотранс РСФСР.– М.: Транспорт, 1986. – 73 с.
ПРИЛОЖЕНИЯ
Приложение 1
Некоторые функции MathCad [14]
| Обозначение функции | Функция |
| APPEND(file) | Добавление значения одиночной переменной к файлу file.dat на диске |
| APPENDPRN(file) | Добавление матрицы к существующему файлу file.prn на диске |
| сеil(х) | Наименьшее целое, не превышающее x |
| cnorm(x) | Интеграл от минус бесконечности до х от функции стандартного нормального распределения |
| cols(A) | число столбцов в матрице А. |
| corr(vx, vy | Коэффициент корреляции двух векторов vx и vy |
| csotr(A, n) | Сортировка матрицы А по столбцу n (перестановка строк по возрастанию значений элементов в столбце n) |
| erf(x) | Функция ошибок |
| exp(z) | Экспонента |
| find(var1, var2,…) | Значения var1, var2 … составляющие решение системе уравнений. Число возвращаемых значений равно числу аргументов |
| floor(x) | Наибольшее целое число, меньшее или равное х, |
| Given | Ключевое слово, работающее в паре с функциями find (minerr) |
| hist(intervals, data) | Гистограмма. Вектор intervals задает границы интервалов в порядке возрастания data — массив данных. Возвращает вектор той же размерности, что и вектор intervals, и содержит число точек из data, попавших в соответствующий интервал |
| if(cond, x у) | X если условие верно, иначе у |
| Intercept(vx,vy) | Коэффициент а линейной регрессии y=a+b·x векторов vx и vy. |
| last(v) | Индекс последнего элемента вектора v |
| lenght(v) | число элементов в векторе v |
| ln(z) | Натуральный логарифм |
| log(z) | Десятичный логарифм |
| max(A) | Наибольший элемент в матрице А |
| mean(v) | Среднее значение вектора v |
| min(A) | Наименьший элемент в матрице А |
| minerr(x1, х2,…) | Вектор значений для х1 х2, … которые приводят к мин. Ошибке в системе уравнений |
| READ(file) | Присваивание простой переменной значения из файла с именем file.prn |
| READPRN (file) | Присваивание матрице значений из файла с именем file.prn |
| root(expr, var) | Значение переменной var при которой выражение expr равно нулю с точностью TOL |
| rows(A) | число строк в матрице А |
| Slope(vx,vy) | коэффициент линейной регрессии y=a+b·x векторов vx и vy |
| sort(v) | сортировка элементов вектора v в порядке возрастания |
| Stdev(v) | стандартное отклонение элементов вектора v |
| tan(z) | Тангенс |
| Until(x,y)=y | прекращение вычислений при x<0 |
| WRITE(file) | отдельное значение, записанное в файл данных под именем file |
| WRITEPRN (file) | вывод матрицы в файл file |
| Г(z) | гамма-функция. (Набирать сочетанием клавиш G+Ctrl+G, |
Приложение 2
Законы распределения непрерывных случайных величин [3, 5, 10]
| Закон распределения | Дифференциальная функция | Интегральная функция | Математическое ожидание | Дисперсия | Параметры распределения |
| Нормальный | 
| 
| 
| 
| tcp-среднее значение s- среднеквадра-тическое отклонение tсм=t1-(t3-t1)/2 - величина смещения |
| Вейбулла | (b/a)(t/a)b-1 × [-exp(-t/a)b] | 1-exp(-t/a)b | a×Г(1+1/b) | a×Г(1+2/b)-(Г(1+1/b))2 | b- параметр формы a- масштабный коэффициент См. приложение. |
| Гамма-распределение | 
| 
| b/a | b/a2 | b= tcp 2 / s2 -параметр формы a=tcp / s2 - масштабный параметр |
| Экспоненциальный (показательный) | l×e-l×t | 1-e-l×t | 1/l | 1/l2 | l=1/ tcp - параметр распределения |
| Эрланга | 
| 
| n/lэ | n/2 | lэ= tcp / s2 - параметр закона Эрланга n= tcp 2 / s2 - порядок распределения Эрланга (целое число) |
Приложение 3
Структурные схемы для расчета безотказности систем
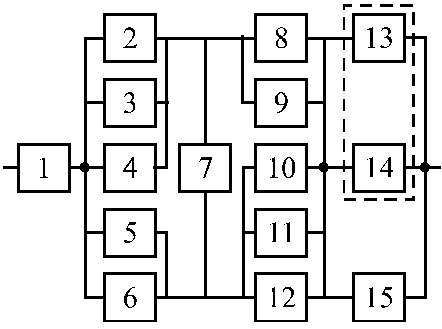
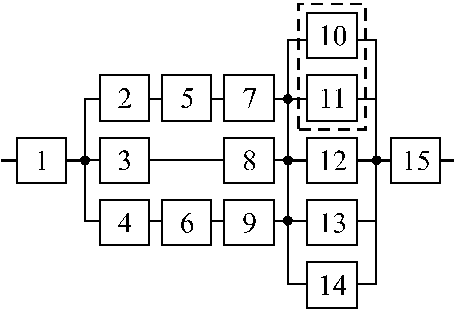
Вариант 1 Вариант 2
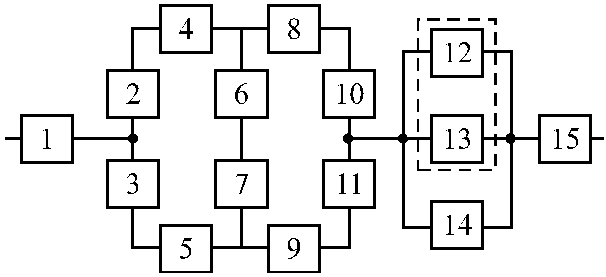
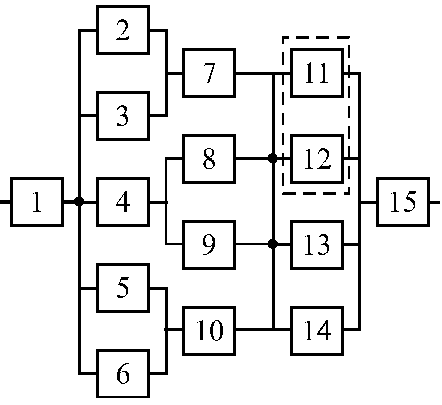
Вариант 3 Вариант 4

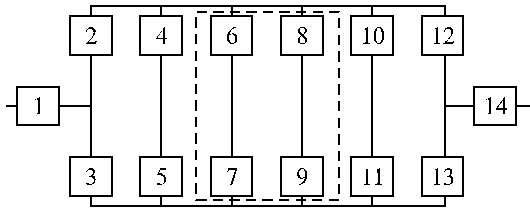
Вариант 5 Вариант 6


Вариант 7 Вариант 8

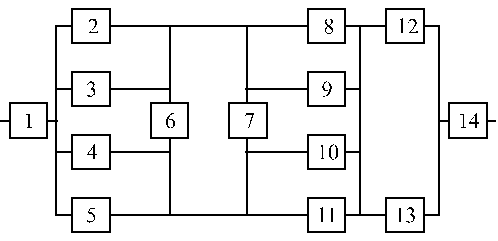
Вариант 9 Вариант 10

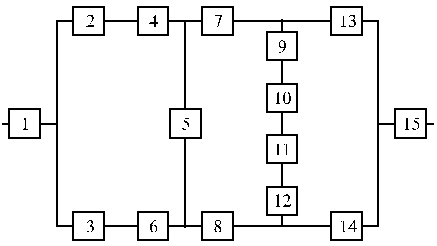
Вариант 11 Вариант 12

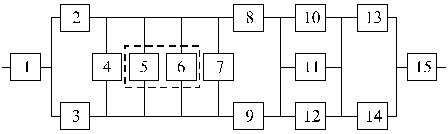
Вариант 13 Вариант 14

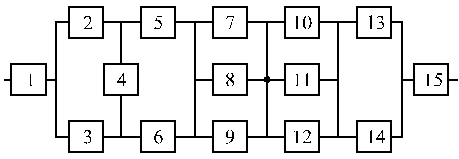
Вариант 15 Вариант 16
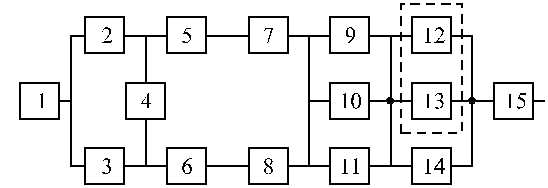
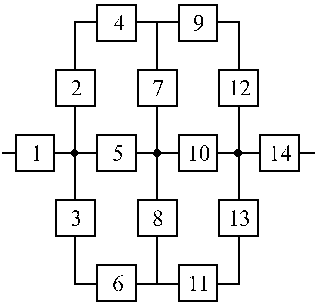
Вариант 17 Вариант 18

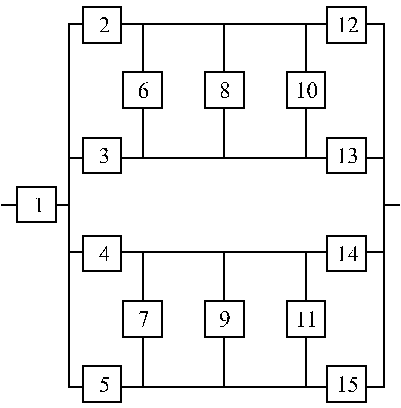
Вариант 19 Вариант 20

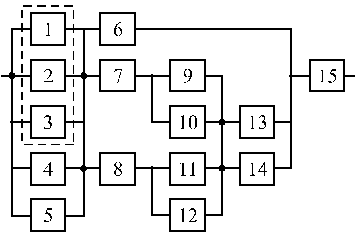
Вариант 21 Вариант 22
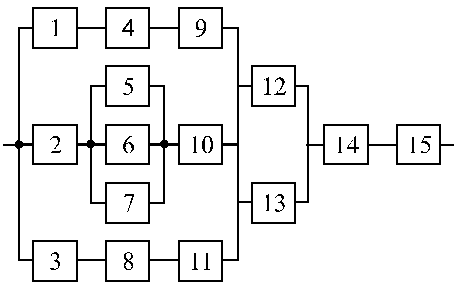
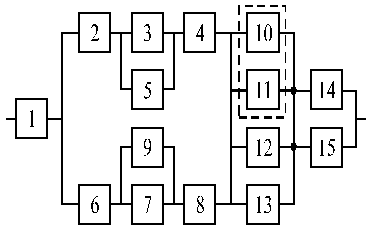
Вариант 23 Вариант 24

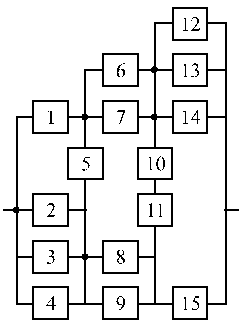
Вариант 25 Вариант 26
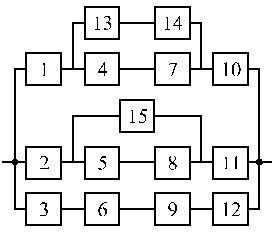
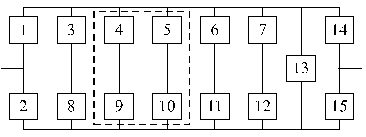
Вариант 27 Вариант 28

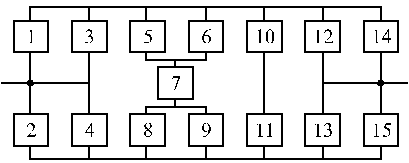
Вариант 29 Вариант 30


Вариант 31 Вариант 32

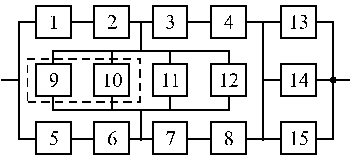
Вариант 33 Вариант 34

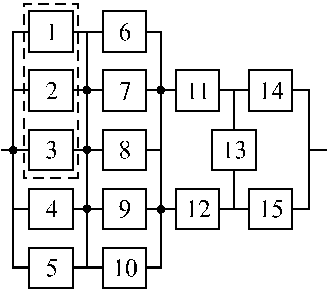
Вариант 35 Вариант 36

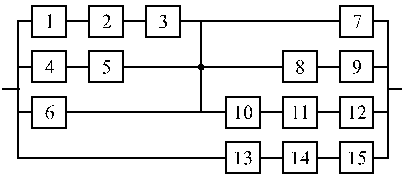
Вариант 37 Вариант 38

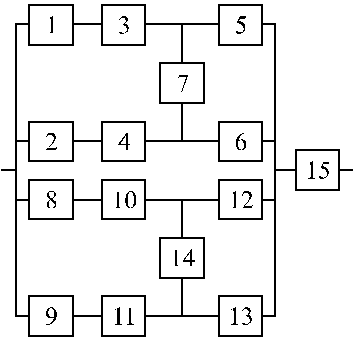
Вариант 39 Вариант 40
Приложение 4
Таблица
Заданные значения показателей надежности
| № | g, | Интенсивности отказов элементов, l i, ´10-6 ч-1 | ||||||||||||||
| вар. | % | |||||||||||||||
| 0,1 | 0,5 | 0,1 | 0,1 | 0,1 | ||||||||||||
| 0,2 | 0,5 | 0,5 | 0,5 | 0,5 | 0,5 | 0,5 | 0,5 | 0,5 | 0,1 | |||||||
| 0,1 | 0,2 | |||||||||||||||
| 0,05 | 0,5 | 0,5 | 0,5 | 0,5 | 0,2 | 0,2 | 0,2 | 0,2 | 0,02 | |||||||
| 0,01 | 0,05 | 0,05 | 0,1 | 0,1 | 0,1 | 0,5 | 0,5 | 0,5 | 0,5 | |||||||
| 0,01 | 0,05 | 0,05 | 0,05 | 0,05 | 0,1 | – | ||||||||||
| 0,05 | 0,5 | 0,5 | 0,5 | 0,5 | 0,05 | 0,05 | 0,05 | 0,01 | 0,01 | 0,1 | 0,2 | 0,2 | 0,1 | – | ||
| 0,1 | 0,5 | 0,5 | 0,5 | 0,2 | 0,2 | 0,2 | 0,01 | 0,01 | 0,01 | 0,5 | 0,5 | 0,5 | 0,1 | – | ||
| 0,03 | 0,5 | 0,5 | 0,5 | 0,2 | 0,2 | 0,2 | 0,03 | 0,03 | 0,03 | 0,1 | – | |||||
| 0,1 | 0,5 | 0,5 | 0,5 | 0,5 | 0,5 | 0,5 | 0,5 | 0,5 | 0,1 | – | ||||||
| 0,05 | 0,2 | 0,2 | 0,5 | 0,5 | 0,5 | 0,5 | 0,5 | 0,5 | 0,5 | 0,5 | 0,5 | 0,2 | 0,2 | 0,1 | ||
| 0,02 | 0,1 | 0,1 | 0,1 | 0,1 | 0,05 | |||||||||||
| 0,01 | 0,2 | 0,2 | 0,2 | 0,2 | 0,1 | 0,1 | 0,5 | 0,5 | 0,5 | 0,1 | – | |||||
| 0,01 | 0,1 | 0,1 | 0,2 | 0,2 | 0,5 | 0,5 | 0,5 | |||||||||
| 0,01 | 0,2 | 0,2 | 0,1 | – | ||||||||||||
| 0,1 | 0,05 | |||||||||||||||
| 0,1 | 0,2 | |||||||||||||||
| 0,01 | 0,1 | – | ||||||||||||||
| 0,1 | 0,5 | 0,5 | ||||||||||||||
| 0,1 | ||||||||||||||||
| 0,1 | 0,5 | 0,5 | 0,5 | 0,5 | 0,2 | 0,2 | 0,5 | 0,2 | ||||||||
| 0,2 | 0,5 | 0,5 | 0,5 | 0,1 | ||||||||||||
| 0,5 | 1,5 | 0,5 | 1,5 | 0,5 | 1,5 | 1,5 | 0,1 | 0,1 | ||||||||
| 0,5 | 0,5 | 0,8 | ||||||||||||||
| 0,5 | 0,5 | 0,5 | 1,5 | 1,5 | 1,5 | 1,5 | ||||||||||
| 0,5 | ||||||||||||||||
| 5,5 | 5,5 | 5,5 | 0,2 | 0,5 | ||||||||||||
| 0,6 | 0,3 | 0,3 | 0,6 | 0,6 | 0,3 | 0,3 | 0,6 | 0,2 | 0,2 | 0,2 | 0,2 | |||||
| 0,6 | 0,6 | 0,6 | 0,6 | 0,6 | ||||||||||||
| 0,5 | 0,5 | 0,2 | 0,2 | 0,2 | ||||||||||||
Приложение 5
Критерий Кохрена. Верхние пятипроцентные критические значения (s=5%) для статистики G построенной по N независимым оценкам дисперсии, каждая из которых обладает n степенями свободы [4]
| n1 | n2 | |||||||||||||
| ¥ | ||||||||||||||
| 0.9985 | 0.9750 | 0.9392 | 0.9057 | 0.8584 | 0.8534 | 0.8332 | 0.8159 | 0.8010 | 0.7880 | 0.7341 | 0.6602 | 0.5813 | 0.500 | |
Приложение 6
Диагностирование электрооборудования двигателя с использованием
мотор-тестера Ц4328
Индивидуальная диагностическая карта объекта диагностирования
Марка шасси, двигателя (тип)......................
N шасси, N двигателя
Наработка с начала эксплуатации................
Наработка (срок службы) после последнего
профилактического мероприятия (ремонта)...
Характеристика последнего отказа................
| Номенклатура диагностических параметров | Величина показателя | Техническое состояние системы | |
| нормативная | измеренная | ||
| 1.Проверка технического состояния аккумуляторной батареи (АКБ) | |||
| а).Напряжение АКБ без нагрузки, В | не < 12 | ||
| б).Напряжение АКБ под нагрузкой, В | не < 10, 2 | ||
| 2.Проверка технического состояния генератора с реле-регулятором | |||
| Напряжение генератора с реле-регулятором, В | 13, 8…14, 6 | ||
| 3.Проверка технического состояния контактов прерывателя | |||
| Переходное сопротивление контактов прерывателя, В | не > 0, 1 | ||
| 4.Измерение угла замкнутого состояния контактов прерывателя, град | |||
| 5.Проверка состояния пружины подвижного контакта | |||
| Приращение угла замкнутого состояния контактов прерывателя, град | не > 3 | ||
| 6.Проверка состояния цилиндро-поршневой группы | |||
| Минимально устойчивая частота вращения коленчатого вала двигателя (КВД), мин -1 | |||
| 7.Проверка эффективности работы цилиндров (развиваемая мощность) | |||
| Падение частоты вращения КВД при отключении цилиндров, %: | |||
| 1-го | |||
| 2-го | |||
| 3-го | |||
| 4-го | |||
| 8.Проверка эффективности работы принудительной вентиляции двигателя | |||
| Падение частоты вращения КВД, мин -1 | 50 и > |
Общая оценка технического состояния объекта (прогноз):
Диагностирование провел (ФИО):
Приложение 7
Показатель функции изменения технического состояния
агрегатов и систем автомобилей
| Параметры | Значения поправочного коэффициента |
| Количество газов, прорывающихся в картер двигателя | 1,3 |
| Угар картерного масла | 2,0 |
| Залегание клапана газораспределения (износ опорных поверхностей тарелки клапана и гнезда) | 1,6 |
| Зазоры в кривошипно-шатунном механизме | 1,2–1,6 |
| Износ кулачков распределительного вала по высоте | 1,1 |
| Радиальный зазор в подшипниках качения и скольжения | 1,5 |
| Износ шлицевых валов | 1,1 |
| Износ валиков, пальцев и осей | 1,4 |
| Мощность двигателя | 0,8 |
| Износ плунжерных пар | 1,1 |
| Износ посадочных гнезд корпусных деталей | 1,0 |
| Износ накладок тормозов и дисков муфт сцепления | 1,0 |
| Износ зубьев шестерен по толщине | 1,5 |
Приложение 8
Номограмма для определения остаточного ресурса деталей, сопряжений, узлов и агрегатов автомобилей
Значения t ocm/ t или R Переход на верхнюю шкалу
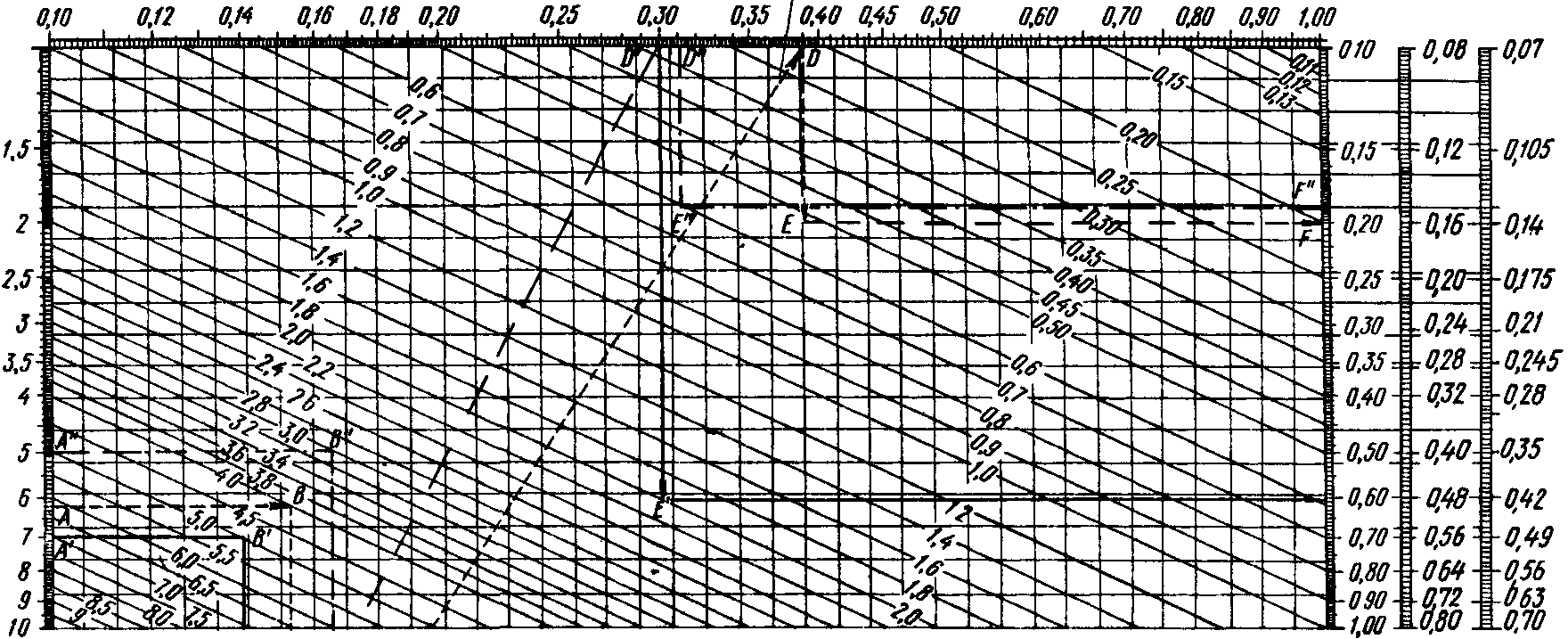
Окончание прил. 8

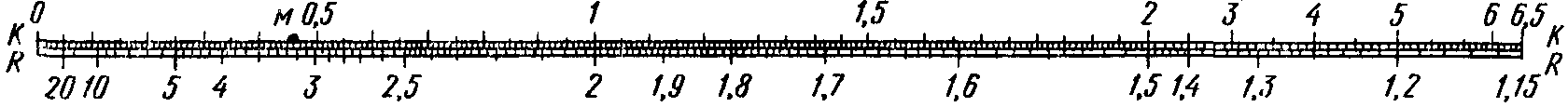
| № вар | км | км | км | км | км | км | км | км | км | км |
| 1. | 16750* | 16345* | 16324* | 16756* | 16123* | |||||
| 2. | 17987* | 17111* | 17324* | 17986* | 17234* | |||||
| 3. | 18000* | 17986* | 18356* | 18354* | 18578* | |||||
| 4. | 18576* | 18756* | 19123* | 18900* | 19123* | |||||
| 5. | 20007* | 21098* | 21365* | 22756* | 21967* | |||||
| 6. | 24820* | 25900* | 26500* | 27320* | 28330* | |||||
| 7. | 34430* | 35500* | 36790* | 38307* | 40100* | |||||
| 8. | 35200* | 36000* | 37100* | 38100* | 40257* | |||||
| 9. | 43410* | 44500* | 45199* | 45300* | 47235* | |||||
| 10. | 47380* | 48926* | 50212* | 52180* | 52345* | |||||
| 11. | 52237* | 52550* | 52600* | 53567* | 54000* | |||||
| 12. | 56900* | 57000* | 58200* | 58689* | 59100* | |||||
| 13. | 57587* | 58213* | 58456* | 59211* | ||||||
| 14. | 60010* | 61876* | 63100* | 63600* | ||||||
| 15. | 63000* | 63987* | 64210* | 64700* | 65421* | |||||
| 16. | 66100* | 66200* | 67000* | 67200* | 68002* | |||||
| 17. | 67200* | 67400* | 67600* | 67720* | 69111* | |||||
| 18. | 68400* | 68769* | 69000* | 69456* | 69678* | |||||
| 19. | 70010* | 71346* | 72671* | 73002* | 73056* | |||||
| 20. | 72400* | 72660* | 72832* | 73330* | 74100* | |||||
| 21. | 73670* | 74561* | 74700* | 75100* | 76000* | |||||
| 22. | 75200* | 75450* | 75923* | 76550* | 77200* | |||||
| 23. | 77432* | 77800* | 78211* | 78899* | 79500* | |||||
| 24. | 78100* | 78450* | 78923* | 81000* | 823400* | |||||
| 25. | 81000* | 81678* | 82178* | 82326* | 83599* | |||||
| 26. | 85000* | 84356* | 86234* | 82000* | 84356* | |||||
| 27. | 93450* | 96450* | 96784* | 91476* | 97450* | |||||
| 28. | 94670* | 93870* | 94760* | 97645* | 93760* |
Приложение 9
Исходные данные для расчета гамма-процентных и средних ресурсов
Приложение 10
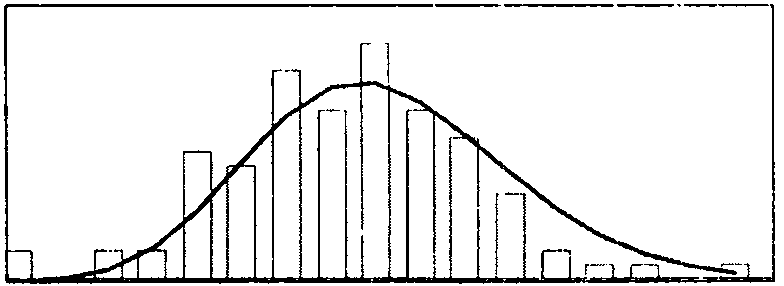
Построение гистограммы распределения
и кривых дифференциальных функций законов распределения
Выбор закона распределения можно произвести визуально, сравнивая гистограмму распределения и кривую плотности распределения.
Исходные данные о наработке приведены в прил. 3 (вектор X). Число данных, их среднее и среднеквадратичное отклонение s определяются по выражениям:
N:= length (X); N:= 100;
t сp:=mean(X); t сp: = 969.909;
s:=stdev(X);  sσ = 196.417.
sσ = 196.417.
Число интервалов гистограммы определяется по формуле
ng:= ceil(l+3.31 n (N)); ng = 25.
Минимальное и максимальное значения случайной величины в статистическом ряду определяются с помощью соответствующих функций векторов:
X min:= floor(min(X)); X max:=ceil(max(X)).
Величина интервала h:= (X max – X min)/ ng.
Значение случайной величины, соответствующей началу j -го интервала:
j:=0… ng; X int:= X min + hj;
k:= 0… ng – l.
Далее создается вектор с числом попаданий случайных величин, содержащихся в массиве Х,в интервал между j -м и (j +1)-м элементами вектора X int:
F:= hist (X int, X).
В заключение строится гистограмма и кривая дифференциальной функции для вышеперечисленных законов распределения. На основании полученных графиков делается вывод о законе распределения случайной величины.
Продолжение прил.10
График плотности нормального распределения
fN (x):= Nh dnorm (x,t ср, s)
| fN (x) |
| х |
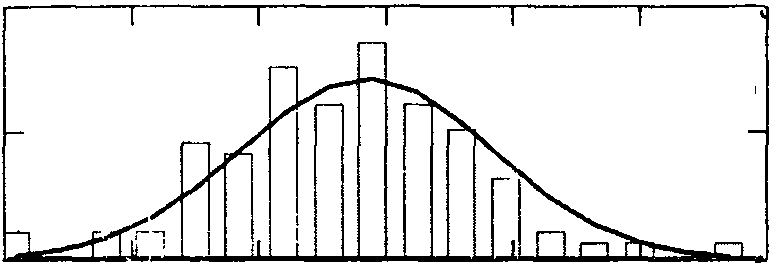
График плотности распределения Вейбулла
FW (x):= Nh (1/a) dweibull (x/a, b)
| fN (x) |
| х |

График плотности гамма-распределения
fG (x):= Nh a dgamma(x a, b)
| fN (x) |
| х |
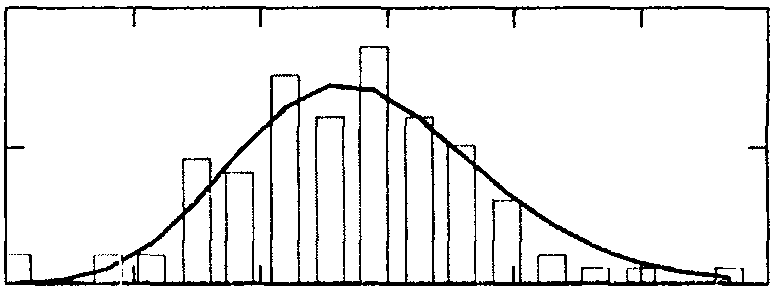
Окончание прил.10
График плотности экспоненциального распределения
FE (x):= Nh dexp (x, l)
| fE (x) |
| х |
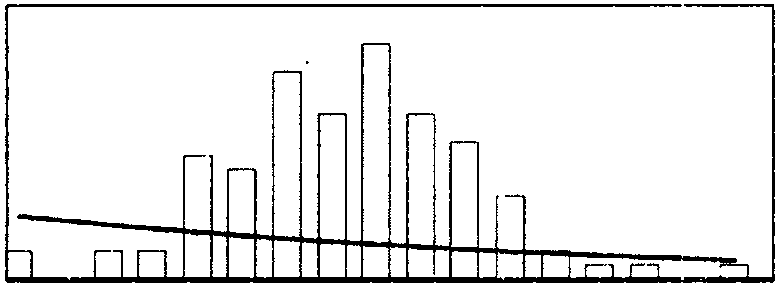
График плотности распределения Эрланга
fER (x):= Nh 
| fER (x) |
| х |
Приложение 11
Проверка гипотез о характере закона распределения
Проверка гипотезы о том, что полученные экспериментально значения данных соответствуют ожидаемым значениям, вычисленным на основе некоторой модели, проводится с помощью критерия c2.
Для правильного применения критерия необходимо, чтобы каждое ожидаемое значение было бы не меньше 5 и сумма наблюдаемых значений должна равняться сумме ожидаемых.
Объем информации N:= 100. Полученный вектор сортируется в порядке возрастания и определяется вероятность возникновения рХ при каждом наработке:
Х:= sort(X); i:= 0.. N – 1; рХ:= (i +1)/(N +0.001).
Рассчитываются значения наработок, соответствующих вероятности рХ для нормального закона распределения XN, закона распределения Вейбулла XW, гамма распределения XG, экспоненциального закона распределения ХЕ, закона распределения Эрланга ХЕr, с использованием функции квантилей законов распределения:
XN:=qnorm (pX, t ср, s); XW:= a- qweibull(pX, b);
XG:= (1/a) qgamma (pX, b); ХЕ:= qexp (pX, l).
Определяются суммы перечисленных векторов, они не должны значительно отличаться:
S X:= 96990.93; S XN:= 97828.127; S XW:= 98176.339;
S XE:= 105027.979; S XG:= 97963.064.
Требуемый уровень значимости e:=0.15.
Число степеней свободы n:= lenpth(X) – I; n = 99.
Рассчитываются оценки для указанных законов распределения:
 – для нормального закона распределения;
– для нормального закона распределения;
 – для закона распределения Вейбулла;
– для закона распределения Вейбулла;
Окончание прил.11
 – для гамма–распределения;
– для гамма–распределения;
 – для экспоненциального закона распределения.
– для экспоненциального закона распределения.
Вероятность совпадения опытных данных с расчетными по критерию c2:
P (c2 >= 0цeнкa c2), допустимая вероятность 10%:
Р:= 1 – pchisq (c2, n)
Рј =  χ
χ
| 0,475 | 99,208 | |
| 0,985 | 71,088 | |
| 9,437 10-14 | 240,254 | |
| 1,416-105 |
Значение c2, соответствующее заданному e:
Х 2:=qchisq (l-a,n); X 2:= 128.382.
| Если Х 2 <c2, то исходная гипотеза должна быть отвергнута: | Х 2<c2= | |
Приложение 12
Характеристики систем технического обслуживания (СМО) [7]
| Характеристики эффективности СМО | Простейшая n -канальная СМО с отказами | Простейшая n -канальная СМО с неограниченной очередью (r ³1) | Простейшая n -канальная СМО с ограничением по длине очереди (m³r ³1) |
| Вероятность отсутствия заявок в СМО Р 0 | 
| 
| 
|
| Вероятность занятости k каналов Pk | j kP 0/ k!(n³k ³1) | j kP 0/ k!(n ³ k ³1) | j kP 0/ k!(n ³ k ³1) |
| Вероятность нахождения в очереди r заявок Pk + r |  (r ³1) (r ³1)
|  (m³r ³1) (m³r ³1)
| |
| Абсолютная пропускная способность A | l×(1- Pn) | l | l(1- Pn + m ) |
| Относительная пропускная способность, Q | 1- Pn | 1- Pn+m | |
| Вероятность отказа P отк | Pn | Pn+m | |
| Вероятность возникновения очереди Р оч | 
| 
|
Окончание прил. 12
| Среднее число заявок в очереди r ср | 
| 
| |
| Среднее число занятых каналов k ср | j(1- Pn) | j | j(1- Pn+m) |
| Среднее число заявок в СМО z ср | r ср+ k ср | r ср+ k ср | r ср+ k ср |
| Среднее время пребывания заявки в очереди t оч | r ср/l | r ср/l | r ср/l |
| Среднее время пребывания заявки в системе t сист | z ср/l | z ср/l | z ср/l |
Приложение 13
Таблица П.13.1
Характеристика условий эксплуатации подвижного состава [13, 22, 28]
| Тип дорожного покрытия | Условия движения | |||||||||||
| за пределами пригородной зоны | в малых городах (100000 чел.) и в пригородной зоне | в больших городах | ||||||||||
| рельеф местности | ||||||||||||
| равнинный | слабохолмистый, холмистый | гористый | горный | равнинный | слабохолмистый, холмистый | гористый | горный | равнинный | слабохолмистый, холмистый | гористый | горный | |
| Цементобетон, асфальтобетон, брусчатка, мозаика | ||||||||||||
| Битумоминеральные смеси | ||||||||||||
| Щебень, гравий, дегтебетон | ||||||||||||
| Булыжник, колотый камень, грунт и малопрочный камень, обработанные вяжущими материалами | ||||||||||||
| Грунт, укрепленный или улучшенный местными материалами, бревенчатое покрытие | ||||||||||||
| Естественные грунтовые дороги, временные карьерные, отвальные дороги, подъездные пути без твердого покрытия |
Таблица П.13.2
Коэффициенты корректирования нормативов
в зависимости от климатического района К3.1 [13, 22, 28]
| Показатель | Природно-климатический район | ||||
| умеренный | умеренный теплый, умеренный теплый влажный, теплый влажный | жаркий сухой, очень жаркий, сухой | холодный | очень холодный | |
| Периодичность ТО | 1,0 | 1,0 | 0,9 | 0,9 | 0,8 |
| Пробег до КР | 1,0 | 1,1 | 0,9 | 0,8 | 0,7 |
| Удельная трудоемкость | 1,0 | 0,9 | 1,1 | 1,2 | 1,3 |
| Расход запасных частей | 1,0 | 0,9 | 1,1 | 1,25 | 1,4 |
Таблица П.13.3
Коэффициент корректирования нормативов в зависимости
от дорожных условий эксплуатации К3.2 [13., 22, 28]
| Показатель | Категория условий эксплуатации | ||||
| Периодичность ТО | 1,0 | 0,9 | 0,8 | 0,7 | 0,6 |
| Пробег до КР автомобилей | 1,0 | 0,9 | 0,8 | 0,7 | 0,6 |
| Пробег до КР двигателей | 1,0 | 0,9 | 0,7 | 0,6 | 0,5 |
| Удельная трудоемкость ТР | 1,0 | 1,1 | 1,2 | 1,4 | 1,5 |
| Расход запасных частей | 1,0 | 1,1 | 1,25 | 1,4 | 1,65 |
Таблица П.13.4
Коэффициент корректирования нормативов трудоемкости ТР
в зависимости от пробега
с начала эксплуатации подвижного состава К4 [13, 22, 28]
Не нашли, что искали? Воспользуйтесь поиском: